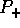 ) is
bounded in the weighted space
) is
bounded in the weighted space 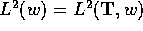 (
( denotes the
unit circle on the complex plane) if and only if the weight
w satisfies the so-called Muckenhoupt
denotes the
unit circle on the complex plane) if and only if the weight
w satisfies the so-called Muckenhoupt 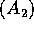 condition,
condition,
F. Nazarov and S. Treil
The goal of this note is to give a very simple proof of the famous
Hunt--Muckenhoupt--Wheeden Theorem. We are going to prove that the
Hilbert transform T (or, equivalently the Riesz projection 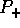 ) is
bounded in the weighted space
) is
bounded in the weighted space 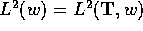 (
( denotes the
unit circle on the complex plane) if and only if the weight
w satisfies the so-called Muckenhoupt
denotes the
unit circle on the complex plane) if and only if the weight
w satisfies the so-called Muckenhoupt 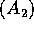 condition,
condition,
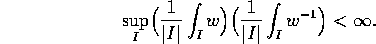
The proof is even simpler that in the paper by Treil and Volbeg A simple proof of the Hunt - Muckenhoupt - Wheeden theorem.
The fanciest technical ``tool'' we are using is Green's formula.
The proof we are presenting looks like a very clever artificial trick. It looks like it is impossible to understand how one can find that kind of tricks. However it is not the case, and there are some very deep ideas behind this elementary proof.