 |
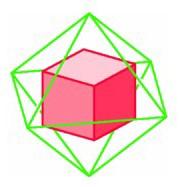 |
The octahedron is dual to the cube (left); the cube is dual to the octahedron (right).
One of the most illuminating ways of constructing a regular dodecahedron is by appealing to the principle of duality. A cube and an octahedron, for example, are very closely related. If we choose the centers of the six square faces of a cube, these are the vertices of an octahedron. We say that the octahedron is the dual of the cube. Conversely, the centers of the eight triangular faces of an octahedron are the vertices of a cube, so the cube is the dual of the octahedron.
| |||
The octahedron is dual to the cube (left); the cube is dual to the octahedron (right). |
What happens if we construct duals of other regular polyhedra? For a tetrahedron, the centers of the four triangular faces form another tetrahedron, so the tetrahedon is self-dual. More thought is required to find the figure having as vertices the centers of the 20 triangles of the icosahedron. Around each vertex of the icosahedron there are five triangles, and the centers of these five triangles when connected form a regular pentagon. The icosahedron has 12 vertices, so we obtain a regular arrangement of 12 regular pentagons, three at each vertex. This is the fifth regular polyhedron predicted by our argument, the regular dodecahedron.
The regular dodecahedron has 20 vertices, with three pentagons at each vertex. The centers of the pentagons will then give 20 equilateral triangles, forming a regular icosahedron. Thus the five regular polyhedra fall into three groups: two dual pairs and one polyhedron that is dual to itself.
| ||||
The self-dual tetrahedron (left); the dodecahedron is dual to the icosahedron (center); the icosahedron is dual to the dodecahedron (right). |
| The Search for Regular Polytopes | ||
| Table of Contents | ||
| The Search for Regular Polyhedra |