 |
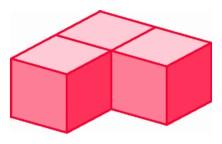
Three cubes around an edge in three-space.
A group of Flatlanders could easily follow Euclid's argument for determining the number of regular polyhedra. They could understand the theorem that there are at most five ways to fit copies of the same regular polygon around a point in their flat space. They would not be able to imagine what it would be like to fold such a configuration up into three-space, but they could still appreciate that there are at most five regular polyhedra in three-space.
Once mathematicians realized they could think about geometry in higher dimensions, they began to look for analogues of polygons and polyhedra. Just as polygons are bounded by segments and polyhedra are bounded by regular polygonal figures, the analogous objects in four dimensions would be bounded by regular polyhedra. Such objects in higher dimensions came to be known as polytopes.
The discovery of all five regular polyhedra in three-dimensional space was well known and well appreciated. It was natural to try to find the analogous result in four-dimensional space, and the "search for the regular polytopes" was on. In the 1880s, the decade in which Abbott wrote Flatland, there was a veritable polytope rush among mathematicians in the United States, Scandinavia, and Germany. At least one reputable mathematician published an incorrect list, and intense argument erupted about who was the first to find all of the regular polytopes. The American contender, William Stringham, analyzed the possible configurations of regular polyhedra around a point in three-space and produced a set of pictures, which were printed in his article in the American Journal of Mathematics. But there were a large number of cases to consider and his argument was incomplete. He was not completely convinced he had found all of the regular polytopes. Fortunately there soon appeared a simpler and more compelling argument.
To understand Stringham's approach, consider the regular figure that we already know very well, the hypercube. It has 16 vertices, with four edges at each vertex. Any three of these edges determine an ordinary cube, so there are four cubes at each vertex. just as we can think of the part of a cube near a vertex as three squares in the plane, with instructions for attaching two edges together in three-space, we may think of the part of a hypercube near a vertex as four cubes in three-space, with instructions for attaching pairs of square faces together. And just as the Flatlanders cannot actually put the three squares together, since they do not have access to our third dimension, we cannot put the four cubes together to form part of the hypercube in four-space, but we can still appreciate the problem.
| ||
Three cubes around an edge in three-space. |
The figure in the margin of this page suggests an approach that simplifies the problem of determining possible regular polytopes in four-space. Instead of examining the many possible ways in which a collection of polyhedra can fit around a vertex, rather consider the number that can fit around an edge. When the sum of the angles of the polyhedra around an edge does not fill the space around the edge, there is room to fold the figure up into the fourth dimension.
The problem of determining how many regular polyhedra fit around an edge turns out to be relatively easy to investigate by experiment. It is clear that one can get three cubes around an edge in three-space, and that four will already fill the region. Therefore, there can be at most one regular polytope with cubical faces, namely the hypercube.
| The Four-Simplex | ||
| Table of Contents | ||
| Duals of Regular Polyhedra |