 |
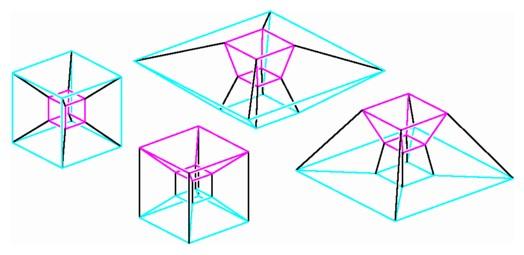
Clockwise starting from the upper left: a sequence of central projections of a rotating hypercube in four-space.
Within a generation of the invention of photography 150 years ago, Eadweard Muybridge had used this new technology to alter our perception of time and space. The photographs of Muybridge himself, striding up a ramp in front of his camera, could be placed on a rotary device and flipped over and over so that he walked on and on, in a primitive version of a motion picture. Slow motion and freeze frame techniques made it possible to analyze the motion of a racehorse or the exertion of muscles in lifting a log.
We can combine a century and a half of animation experience together with modern computer graphics to create and investigate complicated configurations in three-dimensional space. Architectural and industrial design become dynamic processes as we look at not just a few views but 30 views per second, each slightly different from its predecessor, giving the impression of continuous motion. We can experience what it would be like to walk along a corridor or down a staircase in a building that has not yet been constructed. As an architect takes her client on a tour of a prospective auditorium, she can alter the different features to create different impressions. Should this window be placed slightly higher? Should that entranceway be longer? A turn of a dial can produce the new view and simultaneously make the changes for a new set of blueprints.
Modern graphics computers can produce images very quickly. For a wire-frame object, the computer calculates the positions of the vertices and draws the appropriate segments. The speed of production and display depends strongly on the number of vertices and edges in the object. Even on some relatively small machines, a cube, with 8 vertices and 12 edges, can be rotated to give the impression of continuous motion in what is called real time. The hypercube is not that much more complicated, with 16 vertices and 32 edges. A. K. Dewdney described ways of creating programs for hypercube rotation in the April 1986 "Computer Recreations" column of Scientific American.
To create an animation using parallel projection, the program keeps track of the position of one corner of the cube or hypercube and of all corners attached to it by edges. Once the images of these points are determined, all the other points and segments can be drawn easily since the images of parallel segments of the same length will be parallel segments of the same length (as described in Chapter 4). Some additional calculations are necessary for central projections since images of parallel segments will no longer be parallel but will lie in lines going through "vanishing points." The computer is quick enough to carry out these computations to produce frames in perspective of an animation as the hypercube rotates in four-dimensional space. Color-coding makes it possible to keep track of different parts of the rotating hypercube, as portrayed in the film The Hypercube: Projections and Slicing.
The second section of that film begins by showing central projections of the three-cube. In the first sequence, white edges join corresponding vertices of a red square and a green square lying opposite. As the cube rotates in three-space, its images under central projection change until at one point we have a green square inside a red one, then a red trapezoid next to a green trapezoid, and then a red square inside a green square. The analogous sequence for the hypercube (as it is shown in the illustration on the next page) starts with a red cube inside a blue cube joined by black edges stretching between corresponding vertices. The images formed when the hypercube rotates in four-dimensional space resemble those of the ordinary cube rotating in three-space. The large blue cube opens toward the top, flattens out, and opens inward to form an incomplete pyramid, while at the same time the small red cube opens toward the bottom to form another incomplete pyramid. If we continue the rotation, the blue cube will become the small cube, and the red cube will flatten out and come back to become the large cube.
| ||
Clockwise starting from the upper left: a sequence of central projections of a rotating hypercube in four-space. |
In observing such a sequence not once but several times, the viewer gains an appreciation of the symmetry of the hypercube. Each of the eight cubical faces takes its turn holding all of the various positions in the Schlegel polyhedron. As each of the cubes flattens out and opens up again during the rotation, it changes orientation. If a cube were to contain a right-handed glove before the flattening, the glove would have become left-handed afterward, and conversely. This reversal of orientation plays a central role in a famous philosophical dispute, which we will treat in Chapter 9. It also is a common source of ambiguity when we try to interpret moving visual images of objects from four-dimensional space. The more experience we have with understanding simple objects from several standpoints, the better is our chance of understanding images of new objects from four-dimensional space and higher.
| The Polyhedral Torus in the Hypercube | ||
| Table of Contents | ||
| Schlegel Polyhedra for Regular Polytopes |