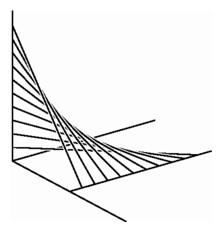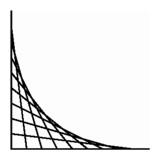
The geometric space of segments is a configuration space with a long history. In this geometry, the fundamental elements are not points but segments, determined by pairs of endpoints. Already studied in the last century as an example of a real four-dimensional geometry, the geometry of segments can describe architectural structures made up of straight boards as well as works of art created by sculptors such as Naum Gabo by stretching strings between frameworks. The fact that the separate pieces of many of Gabo's works can be described by giving simple formulas adds a new element to their beauty, and as we understand how to develop basic shapes in the space of segments, we can appreciate even more the process of artistic creation that assembles these components in such powerful form.

The complexity of the final design often reflects its dimensionality. Consider the following stylized account of a progressively more complicated set of challenges leading to an important four-dimensional geometry of segments in space. For a sculpture show, two artists decide to decorate a wall with a pattern of plastic strings. They come up with a pleasing design by stretching 20 strings from the left-hand edge of the wall down to the baseboard. So that they can put the strings up again later, they have to find a way of recording the string positions. By recording two numbers, they can specify the position of any string. For example, the pair of numbers (4, 3) indicates the string that goes from the point 4 feet over along the floor to the point 3 feet up on the wall edge. Since it takes just two spots to place a given string, the dimensionality of the configuration space is evidently two.

	Left: Two points moving uniformly along coordinate axes determine a two-dimensional geometry of segments. Right: Two points moving along nonintersecting lines in space determine a hyperbolic paraboloid, formed here as a collection of strings.

In a way, constructing a sculpture in the space of segments is like the old game of ``connect the dots.'' In the plane, a polygon is determined by a sequence of ordered pairs, and by connecting the dots in order, we draw the polygon. In the example at upper left, the basic elements are not points but segments, and we are recording a ``polygon of segments.''

We can increase the dimensionality of the collection of strings by allowing the bottom of a string to be placed anywhere on the floor, leaving the top still somewhere on the left edge of the wall. We still need one number for the height, but now the record will include two more numbers for the floor coordinates. The collection of segments is now three-dimensional.

By allowing the strings to start anywhere on the vertical wall and end up anywhere on the floor, we have an actual four-dimensional system. By convention we could specify each line by four coordinates, the first two giving the floor endpoint, and the third and fourth giving the baseboard and height coordinates for the wall endpoint.

An example of a ``curve'' in this geometry might be obtained by connecting points on a vertical line on the wall to a line parallel to the baseboard, moving along the baseboard by a fixed amount each time we move down the upright by a fixed amount. This gives a sequence of segments in space corresponding to a sequence of points in the configuration space. In the configuration space, these points lie along a straight line. In space, the sequence of segments all lie on a familiar architectural element, a hyperbolic paraboloid.

From the space of segments we move to the space of lines. Any segment determines a line, and in fact for each line meeting a pair of planes in distinct points, we find a segment determined by the points of intersection. Thus we may specify the lines meeting the two planes by four coordinates, two for each intersection point, and the space of lines in three-space is four-dimensional.

Calculations can tell us whether or not two strings intersect each other. It is commonplace for strings laid out along a wall to intersect. Such intersections are rare if we choose the lines from among a three-dimensional collection, and rarer still for the four-dimensional system of lines in space.

Whereas the collection of lines in three-space is four-dimensional, the collection of lines in the plane is two-dimensional since we can specify a line not through the origin by telling the points where it intersects the two coordinate axes. This collection of lines in the plane is also related to the collection of planes through the origin in space. To see this, start with a fixed plane not through the origin. Then for almost any plane through the origin, the intersection with this fixed plane is a line. This sets up a correspondence between planes through the origin and lines in a plane, so the set of planes through the origin in three-space is two-dimensional. Similarly, the set of two-dimensional planes through the origin in four-dimensional space is in one-to-one correspondence with the lines in a three-space not going through the origin. This correspondence is at the heart of the subject of projective geometry.

Left: Each line in the horizontal plane at height one corresponds to a plane through the origin in three-space. Right: Four coordinates describe the set of two-dimensional planes through the origin in four-space. Two parallelograms centered at the origin in four-dimensional space may intersect in a single point. In this three-dimensional diagram, points are colored to indicate their height in four-space, so there is just one pair of points with the same fourth coordinate as well as the same first three coordinates.

In the spaces of lines or planes, there always seem to be special cases: lines or planes not specified by any choice of coordinates. Consider for example the two-dimensional space of lines in the plane. If we identify a line by its intersections with a horizontal and a vertical axes in the plane (the ``intercept form''), then we miss those lines that pass through the origin. If we identify a line by its intersections with two vertical lines (the ``slope-intercept form''), then we miss all other vertical lines. Similarly, if we identify lines in space by their intersections with two planes, then if the planes intersect, we miss the lines passing through their intersection line, and if the planes are parallel, we miss all lines lying in other parallel planes. If we are interested in the geometry near any given line, we can choose the reference planes to avoid any problem identifying nearby lines, and in this way we can study the entire projective geometry of the space of lines or planes.

We encounter a similar difficulty finding a valid coordinate system for the entire sphere. In the standard latitude-longitude system, we cannot assign unique coordinates to the north and south poles, where longitude lines converge. These are called the singular points of the chart. If we rotate the sphere while leaving the coordinate lines fixed, then there will be no singular points in the Arctic and Antarctic regions, but some other points of the sphere will now be singular. We do know that we can obtain an atlas, a collection of charts such that every point is a nonsingular point for at least one chart, and such that there is enough overlap between charts so that we can plan a route from any point to any other point. This notion of an atlas of charts is at the heart of the definition of a particular sort of configuration space called a manifold. In this type of space, every point lies in a region having a chart without singularities, and there is sufficient overlap to allow us to compare the geometry at one point to that of another.

Once we set up an atlas of charts on a surface, we can tell when a function on the surface is differentiable, a term indicating that the function can be approximated by the graph of a linear function, producing a line or plane or hyperplane, depending on the dimension. The collection of all differentiable functions is an extremely important feature of the surface, called its differentiable structure. It was found rather early that there was essentially only one possible differentiable structure on the ordinary two-dimensional sphere in three-space, and mathematicians suspected that in general there would only be one differentiable structure on a sphere of any dimension. It was quite a surprise therefore when John Milnor found in 1958 that there were essentially different ways of putting a differentiable structure on the seven-dimensional sphere. It was possible to construct an atlas with a perfectly consistent set of charts, so that one could identify which functions were differentiable, and to compare this collection with the differentiable functions on the ordinary seven-sphere in eight-dimensional space. The two collections were different. Milnor had constructed what he called an exotic differentiable structure on a higher-dimensional sphere, thereby opening up an entire field of study, differential topology.

	A graph of a function describing the surface of a torus in three-space is approximated by the plane tangent to the surface at one of its points.

In spite of the existence of exotic structures on the sphere, mathematicians generally believed that at least the differentiable structure of ordinary space was uniquely determined. This fact had been proven for all dimensions except four, and mathematicians expected that this too would be proved in due course. It was astounding therefore when in the early 1980s the work of two young mathematicians, Michael Freedman and Simon Donaldson, combined to show that the common belief was false--there are infinitely many ways to construct a differentiable structure on four-dimensional space.

			Wave Fronts and Focal Curves in the Plane
			Table of Contents
			The Dimensionality of Stage Lighting