 |
An ellipse and several of its interior parallel curves.
Heaters and loudspeakers affect their surrounding space by radiating waves of heat or waves of sound. The nature of the waves depends on the shape of the object causing them and on its position in space. Many wave sources have the property of focusing waves the way a lens focuses waves of light. Two overlapping branches of mathematics known as geometric acoustics and geometric optics both study the propagation of wave fronts and the focusing properties of curves and surfaces, and in doing so, they bring together the geometry of lines in space and the geometry of circles in the plane.
Waves radiating from a source often interfere with each other, creating focal points. The collections of focal points from the various waves form intricate patterns, increasing in complexity as the dimension of the wave source increases. Once again the dimensional analogy helps us to appreciate these patterns. With a firm understanding of the geometry of focal points for curves in the plane, we are much better able to grasp the far more complicated surfaces of focal points in three-dimensional space. And often it is possible to understand the geometry of a wave source in one space by looking at a higher-dimensional configuration space of lines or circles associated with the object.
The wave patterns are simplest when the source radiating them is the simplest possible object, a point. When we speak into a telephone, our voice acts as a point source causing waves to travel out along the wire. Similarly when we heat the tip of a metal rod, heat travels out along the rod. In each case, a single "point wave" is moving along a one-dimensional space. By coloring each point according to its temperature, we obtain a spectrum along the path of the wave indicating how far it has traveled, from red-hot down to a cold violet. Heating the midpoint of a metal rod sends a heat wave traveling out in both directions. Points equally distant from the source of heat will have the same temperature and therefore the same color.
Moving up to two dimensions, we consider ripples from a pebble tossed into a still pond, or a brushfire spreading out from a lightning strike. The wave fronts will be concentric circles, expanding out in a plane from a single point source. If the point source radiates heat, then points of equal temperature are collected into "isothermal circles," like the isotherms on a weather map, which also connect points of equal temperature. By coloring each circle according to its distance from the origin, we in a sense transform one variable into another.
If the source of heat is a baseboard radiator along a wall, then the points on the floor with the same temperature will lie in lines parallel to the wall. Heat radiates outward in straight waves that never interfere with one another. The lack of interference is a manifestation of the straightness of the line source of the wave.
More interesting patterns emerge if the source is not a point or a line but rather an object with curvature. The simplest example occurs when a wave travels out from a circle in the plane. If we strike a metal circular cylinder immersed in a still pond, we send a pair of shock waves moving along the surface of the water. One shock wave merely continues outward in an ever-expanding set of nonintersecting concentric circles. The other wave moves inward toward the center. At the very center, the wave shrinks down to a single focal point and reemerges as another circle with the same center, heading outward and eventually passing through the cylinder. The waves will cover each point other than the center exactly twice. The color coding is not quite so effective as in the case of a point source or line source since it is no longer true that each point has a unique color.
We can use color in another way to indicate what is happening as the inner circle shrinks down to a point and reappears. If we color each point of the original circle according to the usual color wheel, then the points are labeled red, orange, yellow, green, blue, and violet as we move counterclockwise around the circle. As the wave front moves inward from this circle, each point moves in a straight line. After these colored lines come together at the focal point and then reemerge, the red point is directly opposite its starting point, to the far left rather than the far right. Each colored point on the wave front is directly opposite its starting point, so the circle has turned itself inside out in the process of passing through its focal point.
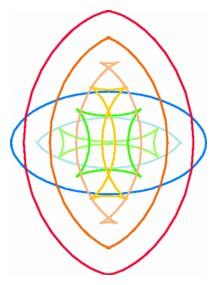
The behavior of waves is far more complex when they originate from a curve having varying curvature, like an ellipse. To represent the region swept out by the parallel waves shortly after they leave the ellipse, we draw circles of the same small radius centered at the points of the ellipse. The boundary of the region covered by this collection of discs is a pair of parallel curves to the ellipse. One parallel curve continues outward, yielding a family of curves that never interfere with one another. They appear nearly elliptical in shape, although they are not exactly ellipses.
| ||
An ellipse and several of its interior parallel curves. |
The inner parallel curve on the other hand behaves very differently. Shortly after it moves in toward the center, the parallel curve develops singularities, cusplike points where the curve abruptly changes its direction. Although in the case of a circle, an entire parallel curve collapsed to a point in one instant, in the case of the ellipse, the focusing takes place at different times. The first singularities appear near the most tightly curved points of the dark blue ellipse. At one instant, the innermost light blue curve appears to have two sharp-angled corners. These corners immediately spawn a pair of ``fishtails,'' so that the parallel curve now has four sharp cusp points and a pair of double points where the parallel curve cuts through itself. As the parallel curve continues farther, the double points coalesce to a single point (light green) and then disappear, leaving a dark green curve with four cusps and no crossing points. A bit farther along, two arcs come together to form a parallel curve having a pair of double points and four cusps (yellow and light orange). The two pairs of cusps then merge with the double points (dark orange), and after this stage, the parallel curve once again becomes a singularity-free red curve resembling an ellipse. During this process, the ellipse has completely turned itself inside out.
If we display a collection of the parallel curves all on the same diagram, we see a new phenomenon that might be difficult to identify if we only saw the individual parallel curves' the cusps of the curves parallel to the ellipse trace out another curve, the focal curve or evolute of the ellipse. If we know a curve well enough to generate its parallel curves, then we may obtain the focal curve as the collection of all cusp points on all parallel curves.
We get a new insight into the geometry of this important focal curve by changing our viewpoint. Instead of thinking of parallel curves emanating all at once from an original curve, we may think of rays perpendicular to the curve proceeding from a number of points spaced out along the curve. We can imagine each of the patrons seated at the rim of an ellipsoidal stadium pointing a laser in the direction straight out from the rim. Viewed from a blimp high above the stadium, the light rays would interfere with each other to create a bright curve called the light caustic by researchers in mathematical optics. It is identical with the focal curve.
In the case of a circular stadium, all of the rays coming out from points of the rim will coalesce at a single point, and the evolute degenerates to a single point. If the circle deforms to an ellipse, this degenerate evolute opens out into a curve.
The characteristics of the evolute curve tell us something about the way that the curvature changes as we go around the ellipse. For example, the evolute has the same symmetries as the original ellipse. It has its own singularities, two cusps on the major axis of the ellipse and two cusps on the minor axis. The rays coming from the points of the ellipse cover some parts of the plane twice and other parts four times. The evolute curve separates the region of twofold coverage from the set of points covered four times.
By adding a third dimension, we can display the same phenomena more clearly. If the patrons on the rim of the stadium shine their laser lights not straight ahead but up at a 45-degree angle, the rays will form a pattern in the space above the stadium. From the viewpoint of a blimp high above the stadium, the pattern looks the same, but from the side we see a far more intriguing configuration. The rays intersect one another to form lines of double points, and they interfere with each other to form bright curves of cusps. At certain points, arcs of double points come together with arcs of cusps to form even more complicated singularities. Strips of light radiating outward from positions spaced along the rim of the stadium interlace like the fingers of two hands coming together. If we send up lights from all points of the rim, they form a surface of rays, known in geometrical optics as ``the catastrophe surface of the normal mapping.''
| ||
Horizontal slices of the catastrophe surface give parallel curves of the ellipse displaced in space. |
This surface with its curves of singularities holds the history of all the parallel curves of the original curve. We can obtain the different parallel curves of the ellipse by slicing this surface with horizontal planes. A curve at one level is just the corresponding parallel curve lifted out of the plane a distance equal to its planar distance to the original ellipse. When the horizontal slice goes through one of the two arcs of double points, the corresponding parallel curve has a pair of double points. When it goes through a cuspoidal curve on this surface, the corresponding parallel curve will have a cusp at that point.
We can relate this construction back to the three-dimensional Laguerre geometry of circles in the plane, mentioned earlier in this chapter. In that geometry, a point in three-space corresponds to the circle centered at the point in the horizontal plane specified by the first two coordinates, with its radius given by the third coordinate. The points of a 45-degree line perpendicular to a horizontal line at a point correspond to circles in the plane that are tangent to the line at the point. Therefore, the collection of these 45-degree lines forming the catastrophe surface of a curve corresponds to the collection of circles that are tangent to the curve at at least one point. A great deal of the geometry of the curve is contained in this surface. For example, the double point curve, where the catastrophe surface intersects itself, corresponds to the collection of circles that are tangent to the curve at two or more points.
We can return to gain a new insight into previously understood cases by deforming the ellipse back into a circle. The rays moving up at a 45-degree angle will move along during the deformation, until the entire focal behavior spread out in the case of the ellipse coalesces to a single point, the origin of a double cone. We can think of the focal curve of the ellipse as a perturbation of this highly singular conical point. This picture of a conical point will be useful to us later on in our investigations of surfaces of revolution.
| Wave Fronts in Three-Dimensional Space | ||
| Table of Contents | ||
| Configuration Spaces of Segments and Lines |