 |
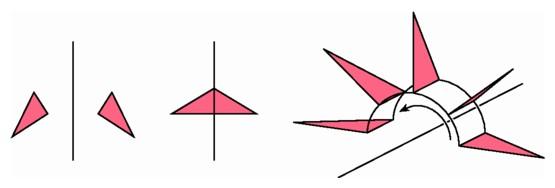
When a scalene triangle is reflected across a line (left), the triangles cannot be superposed in the plane (center); by rotating a scalene triangle about a line in space, we can superpose it on its reflected image (right).
It was not only the emergence of new axiom systems of non-Euclidean geometry that upset the followers of Immanuel Kant. Another serious point of contention centered around a different geometric notion, orientability. In the plane we say that two figures can be superposed if it is possible to slide one to the exact position occupied by the other. Imagine two figures drawn on transparent plastic: sheets able to glide over one another. The two figures could be superposed if we could position one directly on top of the other.
According to traditional geometry, if two figures could be superposed, they were directly congruent, but not every pair of congruent figures could be superposed merely by sliding. One of Euclid's main theorems about triangles says that if the lengths of the sides of one triangle equal those of another, then the two triangles are congruent. But consider a right triangle with three different side lengths and its reflected image in a line (the Flatland equivalent of a full-length mirror). Corresponding sides of the object have the same edge lengths, but it is impossible to superpose them by sliding along the plane. Indeed, if we slide one of the triangles so that two edges of the same length come together, then the two triangles lie on opposite sides of the line containing their common edge.
| ||
When a scalene triangle is reflected across a line (left), the triangles cannot be superposed in the plane (center); by rotating a scalene triangle about a line in space, we can superpose it on its reflected image (right). |
Kant would say that these two triangles are an enantiomorphic pair, congruent but not superposable. It is clear that this notion depends in an essential way on the geometry of the plane. If we consider the two triangles as situated in space, then it is quite easy to pick one up and place it down on the other, like turning the pages of a book.
| ||
Mirror-image off-center pyramids are congruent but not superposable. |
It follows that the definition of enantiomorphic pair depends on the dimension of the space we are working in. This fact becomes crucial when we consider enantiomorphic pairs of objects in three-dimensional space. Instead of a right triangle, consider an off-center pyramid cut from a corner of a rectangular parallelepiped having edges of three different lengths. We can cut off another corner to obtain an off-center pyramid that has the same side lengths for each of its edges. The corresponding triangles in the two pyramids are congruent, but still the pyramids themselves are not superposable. They are mirror images of one another, and they have different "handedness."
The example Kant used was a marble hand broken off a statue. We can easily determine if the hand is a right or a left by attempting to shake hands with it with our right hand. If we succeed, the marble hand is also a right hand; otherwise it is a left hand. But what if we can't get close to the hand? How can we determine whether it is a right hand or a left? Kant set up a more extreme thought experiment--what if the marble hand were the only object in the universe? Would it make sense to say that it is still either a right hand or a left?
In a sense the problem vanishes completely if we do not restrict ourselves to three-dimensional space. In the same way that a triangle can be turned into its mirror image by a rotation about a line in three-space, a marble hand can be turned into its mirror image by a rotation about a plane in four-space. Just as it does not make sense to ask whether a free-floating cutout of a handprint, on a sheet of paper with both sides identical, is a right or a left handprint, so we cannot make sense of the question of whether a marble hand floating freely in four-space is right or left. This answer does not please the followers of Kant even to this day.
| Möbius Bands, Real Projective Planes, and Klein Bottles | ||
| Table of Contents | ||
| Higher-Dimensional Euclidean Geometry |