 |
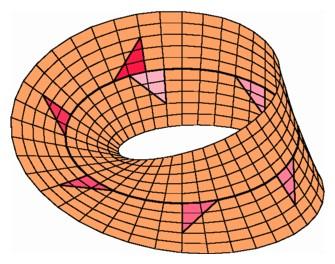
On a Möbius band, a scalene triangle and its reflected image can be superposed.
There is another way to create nonorientable objects, not by changing the dimension but by altering the shape of the space. In 1840 August Möbius invented the surface bearing his name, the Möbius band. It is constructed by pasting together the two vertical edges of a long rectangle, but with a twist so that the, top vertex on one side is connected to the bottom vertex on the other. The resulting surface has only one edge. We should think of the band as made of some porous material through which an ink-drawn figure bleeds, leaving us no way to tell on which side of the strip the figure was originally placed. A triangle drawn on, or rather in this two-dimensional strip can slide along the strip and come back so that it is superposed on its mirror image. There are no enantiomorphic pairs on a Möbius band.
| ||
On a Möbius band, a scalene triangle and its reflected image can be superposed. |
The Möbius band is an example of a nonorientable space, which means that it is not possible to distinguish an object on the surface from its reflected image in a mirror. A surface will be nonorientable precisely when it contains one of these orientation reversing paths. It would be quite a shock to the inhabitants of Flatland if some explorer returned from an expedition with all his right-handed tools transformed into left-handed ones. This scenario is developed at length in an excellent treatment of alternate geometries called The Shape of Space, by Jeffrey Weeks, giving an introduction to the research program of William Thurston. Since we do not really know all that much about the large-scale structure of our universe, it might be possible for some future interstellar explorer to discover an orientation-reversing path in our own three-dimensional space, permitting all of our monkey wrenches and marble right hands to be transformed into left-handed objects. This would dismay the future followers of Kant.
Two important surfaces containing Möbius bands can be built in four-dimensional space. Both have the important property of being without a boundary, like the surface of a sphere. The first, called a real projective plane, is obtained by attaching the boundary of a disc to the boundary of a Möbius band. The second is formed by attaching two Möbius bands along their common boundary to form a nonorientable surface called a Klein bottle, named for its discoverer, Felix Klein.
We have encountered the real projective plane earlier in this chapter in our discussion of elliptic geometry. There we started with the southern hemisphere and we had to imagine attaching together opposite points on the equator. As we can see by considering a thin strip around a great circle arc through the south pole, the ends of the strip on the equator must be attached with a twist, forming a Möbius band. The remainder of the southern hemisphere consists of two half-discs that fit together to form a disc with its boundary attached to the boundary of the Möbius band. Thus, the space of elliptic geometry--the southern hemisphere with each point on the equator attached to its opposite point--can be described as a disc attached to a Möbius band, and therefore as a real projective plane.
| ||
The real projective plane can be thought of as half an icosahedron with opposite segments attached with a twist. |
One of the easiest ways to imagine building any surface is to picture it made out of triangles. Instead of using a hemisphere of a round sphere, we can attempt to build a real projective plane by using the ten triangles in half a regular icosahedron. This half icosahedron has a boundary consisting of six edges, and each edge is to be attached to the opposite edge with a twist, leaving a boundary of three vertices. As there are also three visible vertices not on the boundary, we obtain a representation of the real projective plane using just six vertices and ten triangles. A strip of five triangles stretching from one boundary segment to the opposite segment forms a Möbius band when its end segments are attached with a twist. The Möbius band contains five of the six vertices, and the remaining five triangles fit together to define a disc around the sixth vertex.
In order to try to construct the real projective plane in three-space, we can build a five-vertex Möbius band by choosing five triangles in the projection of a four-simplex, as indicated in the illustration below. The boundary of this hand will consist of a pentagon in space. In order to attach the remaining five triangles without running into the triangles already placed, we have to locate a point from which we could see all five edges of the pentagon, unobstructed by previously chosen sides. It turns out to be impossible to find such a viewing point in three-dimensional space, but it is easy if we are willing to go to four-space. Just as we in three-space can see all rooms of a Flatland house, from a four-dimensional vantage point we could see all points in three-space simultaneously. Thus we can form the five remaining triangles without running into any triangles of the band by connecting all five edges of the boundary of the Möbius band to a point in four-space. Therefore, it is possible to construct a real projective plane in four-space, although it cannot be done in three-dimensional space. We can obtain an even more symmetrical example of a real projective plane by taking ten of the equilateral triangles determined by the six vertices of a regular five-simplex embedded in five-dimensional space. A powerful theorem states that no surface without a boundary and containing a Möbius band can be constructed without self-intersection in three-space. The reason is rather subtle, but it becomes clearer if we use a dimensional analogy. In a Möbius band, it is possible to find two closed curves that cross at one point, something that is impossible in the plane where pairs of curves always cross at an even number of points. Therefore we can conclude that it is impossible to construct a Möbius band in the plane. Now for a Möbius band in three-space, it is possible to follow along very close to the center curve and end up on the other side of the band, just opposite the starting point. If we then pierce through the band with a segment, we obtain a closed curve in space that meets the band at one point. If the band were part of a surface without boundary, like a Klein bottle or a projective plane, then this construction would yield a curve in three-space intersecting such a surface in one point. But in three-space any closed curve must intersect any surface without boundary in an even number of points. Therefore it is impossible to construct any boundaryless nonorientable surface without self-intersection in ordinary three-space.
| |||
Left: To construct the real projective plane, connect the boundary of a five-triangle Möbius band to a point. Right: A closed curve in space near the center of a Möbius band meets the band an odd number of times. |
Another extremely important nonorientable surface is the Klein bottle. The instructions for building a Klein bottle are simple enough: start with a rectangle and attach the vertical sides with a twist and the horizontal sides without a twist. We can follow one instruction or the other but not both. Since the instructions describe a surface without a boundary but containing a Möbius band, we know by the argument in the previous paragraph that we cannot construct a Klein bottle without self-intersection in three-space. The reader will not be surprised to learn, however, that we can construct one in four-space. One way is to start with the five-vertex Möbius band described above and to move it in a direction perpendicular to three-space until it reaches a parallel Möbius band. During this movement, the five edges in the pentagonal boundary of the Möbius band trace out five squares joining the boundary of one Möbius band to the other, thus forming a Klein bottle constructed in four-space without self-intersection.
| |||
Left: The instructions for a Klein bottle are to attach the top and bottom edges of a rectangle to form a cylinder, and to attach the left to the right side with a twist to form a Möbius band. Right: Folding the top edge of the rectangle forward and the bottom edge backward forms a figure eight cylinder, passing through itself along a segment. |
Here are two Movies of the Klein Bottle.
For many years, people attempted to build representations of Klein bottles without self-intersection in ordinary space, and in each case they had to make a compromise and allow the surface to pass through itself. Glassblowers fashioned Klein bottles in space by allowing a tubular portion of the surface to intersect a ring-shaped area on the surface. The sculpture that opens this chapter is a fine recent example of this construction. Another construction was suggested by our work in four-dimensional geometry, where we start to build the Klein bottle not by making a round cylinder but by allowing the cylinder to pass through itself to form a "figure eight" cylinder. We can then attach the figure eights at the ends with a twist to accomplish the identification required to make a Klein bottle. When modeling surfaces on a computer screen, it turns out to be easier to describe this figure eight Klein bottle than the glassblower's version. The modern graphics computer makes it possible for us to design these intriguing objects in four-dimensional space and then investigate them by projecting them into our own viewing space, a fitting final insight in our project of visualizing dimensions.
| Table of Contents | ||
| Immanuel Kant and Nonorientability |