Labware - MA35 Multivariable Calculus - Three Variable Calculus

The moment of inertia I of an object about an axis of rotation is a value which indicates the resistance of that object to changes in rotation about that axis. For a three-dimensional region D with density ρ(x, y), this calculated using the following formula:

I = ∫(r(x, y, z))²ρ(x, y, z)dxdydz

Where r(x, y, z) is the distance of the point (x, y, z) from the axis of rotation.

For an object of density 1, the moment of inertia will be the density multiplied by the integral

I = ∫(r(x, y, z))²dxdydz.

Demos

Moment of Inertia

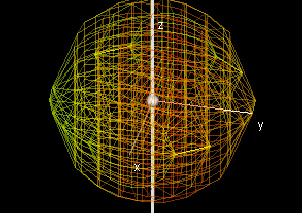
This demo finds the moment of inertia for a three-dimensional region of uniform density. The bounds of z are expressed as functions of x and y, and the bounds of y are expressed as functions of x.
The graph shown displays the region, coloring each point based on its distance from the axis of rotation. The closer a point mass is to the axis of rotation, the less it adds to the moment of inertia.

Exercises

1. Find the moment of inertia of a sphere of radius 1 and uniform density 1 rotated about an axis which passes through its center.

2. Find the moment of inertia of a sphere of radius R, uniform density, and total mass M rotated about an axis which passes through its center.

3. Find the moment of inertia of a cylinder of radius 1 and uniform density 1 rotated about an axis which passes through its center, such that the cylinder rotates as a wheel would rotate.

4. Find the moment of inertia of a cylinder of radius R, uniform density, and total mass M rotated about an axis which passes through its center, such that the cylinder rotates as a wheel would rotate.

5. Compare your result from question 4. to the moment of inertia of a circle of radius R, uniform density, and total mass M rotated about its center.