|
Fundamental Theorem of Calculus
Text Part I: If f(x) is continuous and F(x) = ∫0x f(t) dt, then F'(x) = f(x).

Proof.
\begin{array}
F(x + h) - F(x) & = & \int_0^{x+h} f(t) dt - \int_0^x f(t) dt \\
& = & \int_0^x f(t)dt + \int_x^{x+h}f(t) dt - \int_0^x f(t) dt \\
& = & \int_x^{x+h} f(t) dt \\
& = & f(x) h ,
\end{array}
\[ \frac{F(x + h) - F(x)}{h} = f(x), \]
\[ \lim_{h \to 0} \frac{F(x + h) - F(x)}{h} = f(x), \]
\[ F'(x) = f(x). \]

Part II: If f is continuous and G is an antiderivative of f (i.e. G'(x) = f(x)), then ∫ab f(x) dx = G(b) - G(a).

Proof.
\[ \int_a^b f(x) dx = \int_0^bf(x)dx - \int_0^a f(x) dx = F(b) - F(a). \]
Let be an antiderivative of , so that .
\[ (F - G)'(x) = F'(x) - G'(x) = f(x) - f(x) = 0 \Rightarrow G(x) = F(x) + C, \]
where C is a constant.
\[ \int_a^b f(x) dx = F(b) - F(a) = (G(b) + C) - (G(a) + C), \]
\[ \int_a^b f(x) dx = G(b) - G(a). \]

Consider a function of one variable, f(x). We saw in lab 1.4.2 that the area under the curve f(x) can be written as a Riemann integral. This yields a second function, F(x), which gives the area under f(t) with 0 ≤ t ≤ x. Explicitly, we write F(x) = ∫0x f(t) dt. It turns out that there is a relationship between this area function of f(x) and the antiderivative of f(x). The theorem that unites the Riemann integral with the concept of antiderivative is known as the Fundamental Theorem of Calculus.
Demos
Fundamental Theorem of Calculus

| 
|
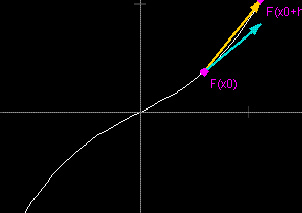
In this demonstration you may type in a function f(x) in the control panel. This function appears in the window titled "Graph: f(x)". Along the x-axis, slide the red hotspots to choose points x0 and x0 + h. The demonstration shows the area under f(x) for this interval in yellow and the approximating rectangle in green. If F(x) is the corresponding area function of f(x), as defined above, then the yellow area is equal to F(x0 + h) - F(x0). Meanwhile, the area of the rectangle is equal to h f(x0). These two areas are calculated and displayed in the control panel. Notice that as you make h smaller, the yellow area and the area of the rectangle approach each other. The second graph window plots the area function F(x). Two vectors are drawn at F(x0): the orange vector is (h, F(x0 + h) - F(x0)) while the cyan vector is (h, h f(x0)). We know that as h get smaller and smaller the slope of the orange vector approaches F'(x). Notice that the slope of the orange vector also approaches the slope of the cyan vector, which is f(x). 
|
|