|
Change of Order of Integration
(Page: 1 | 2
) Text Fubini's Theorem states that for a continuous function of x and y with a rectangular domain, one can evaluate a double integral by first integrating with respect to x (treating y as a constant) and then integrating this result with respect to y (treating x as a constant), or by first integrating with respect to y (treating x as a constant) and then integrating this result with respect to x (treating y as a constant).

Formally, for a function f(x, y) with domain R such that a ≤ x ≤ b, c ≤ y ≤ d,
∫ab∫cdf(x, y)dydx = ∫cd∫abf(x, y)dxdy = ∫∫Rf(x, y)dA

Demos
Change of Order of Integration

| 
|
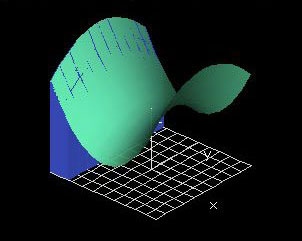
The "Function Graph: f(x,y)" window shows the graph of z(x,y) = -0.5x - 0.5y + 1.
The stepX and stepY variables determine the position of the two sweeping cross sections and are controlled by "tape deck" controllers.
There are two ways to perform the double integration: You can either sweep out along the x-axis, and then let the resulting area sweep along the y-axis (this is called first summing or integrating over x, and then over y). The other possibility is to first integrate over y and then integrate over x. This demo shows that the order of the summation/integration does not change the actual value of the integral. No matter which variable you choose to sum over first, you will always get the same volume under the function graph. 
|
Slab Approximations

| 
|
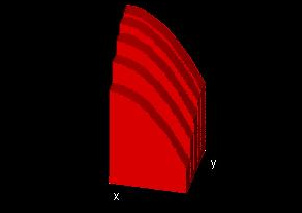
One useful way to think about the evaluation of double integrals is to consider a series of slabs. For y-constant slabs, the height of any slab at some point(x, y0), where y0 is the constant value of y for that particular slab, is given as f(x, y0), so the area of the non-rectangular side of the slab is ∫x(min)x(max)f(x, y0)dx. The slab has a small width in the y direction. We can approximate the volume under the function graph by adding up the volumes of the slabs, a calculation which is equivalent to the summation of an integral. As the number of slabs approaches infinity (and their width becomes infinitessimally small), the summation of the integral becomes an integral of an integral.
x-constant slabs work in the same way, but the order is switched -- a manifestation of Fubini's Theorem.
In this demo, you have the option of viewing the x-constant and y-constant slabs for a function f(x, y). You can vary the number of slabs by changing "xRes" and "yRes". 
|
Exercises The "Slab Approximations" demo description mentions that the series of slabs represents the summation of an integral. Would it be possible instead to take the integral of a summation and get the same result? Compare and contrast these two processes.
|