The Problem
Convex Quadrilaterals
Area
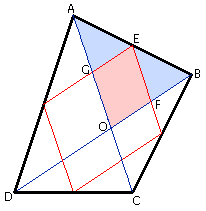
For convex quadrilaterals, the midpoint polygon is a parallelogram with sides parallel to the diagonals (See Figure 1). The diagonals divide the original quadrilateral up into four triangles. If we consider one of these triangles, say ABO, it is clear that the portion of the midpoint polygon contained within the triangle (shaded red) has exactly half the area of the entire triangle (red and blue regions). Therefore the total area of the midpoint polygon, is 1/2 the area of the original quadrilateral
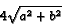 .
.

Figure 1. Finding the area of a midpoint quadrilateral
Perimeter
The perimeter question is more complicated. For a square, the midpoint polygon is a square with sides one over the square root of 2 times the sides of the original square, so the perimeter ratio is 1/sqrt(2), about .7071. More generally, for a rectangle with sides 2a and 2b, the perimeter of the midpoint parallelogram is
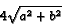 .
.
The perimeter ratio is then
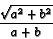 ,
,
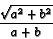 ,
,
so if a = 3 and b = 4, the ratio is 5/7=.714285 and repeating. The ratio is not constant. In general, the length of the midpoint parallelogram is equal to the sum of the lengths of the two diagonals.
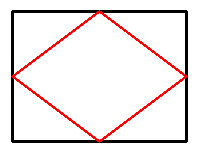

Demonstration 2. Perimeter ratio for rectangles
It is interesting to calculate what the perimeter ratios can be for rectangles. Some experiment suggests that the ratio
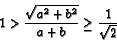 ,
,
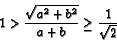 ,
,
since this is equivalent to
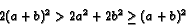 ,
,
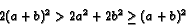 ,
,
which in turn is equivalent to
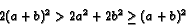 .
.
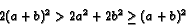 .
.
The minimum is achieved for a square.
At this point we can go in two directions. We can ask about non-convex quadrilaterals, and we can go further to ask about self-intersecting quadrilaterals. Or we can move up to pentagons.