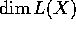 , and Lang's conjecture implies that if K is a number field, and
if
, and Lang's conjecture implies that if K is a number field, and
if 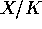 has positive Lang dimension, then
has positive Lang dimension, then 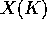 is not Zariski - dense in
X. In [H1], J. Harris proposed a complementary statement:
is not Zariski - dense in
X. In [H1], J. Harris proposed a complementary statement:



As mentioned above, we define the Lang dimension of a variety X to be
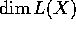 , and Lang's conjecture implies that if K is a number field, and
if
, and Lang's conjecture implies that if K is a number field, and
if 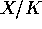 has positive Lang dimension, then
has positive Lang dimension, then 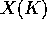 is not Zariski - dense in
X. In [H1], J. Harris proposed a complementary statement:
is not Zariski - dense in
X. In [H1], J. Harris proposed a complementary statement:
It is illuminating to consider the motivating case of an elliptic surface of positive rank.
Let 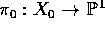 be a pencil of cubics through 9 rational points in
be a pencil of cubics through 9 rational points in
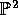 . By choosing the base points in general position we can guarantee that
the pencil has 12 irreducible singular fibers which are nodal rational
curves. The Mordell - Weil group of
. By choosing the base points in general position we can guarantee that
the pencil has 12 irreducible singular fibers which are nodal rational
curves. The Mordell - Weil group of 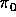 has rank 8. The relative dualizing
sheaf
has rank 8. The relative dualizing
sheaf 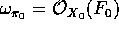 where
where 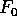 is a fiber. Let
is a fiber. Let
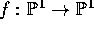 be a map of degree at least 3. Let
be a map of degree at least 3. Let 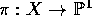 be
the pull-back of
be
the pull-back of 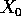 along f. Then
along f. Then 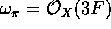 , therefore
, therefore
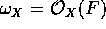 and X has Kodaira dimension 1. The Iitaka fibration is
simply
and X has Kodaira dimension 1. The Iitaka fibration is
simply  . The elliptic surface X still has a Mordell - Weil group of rank
8 of sections. By applying these sections to rational points on
. The elliptic surface X still has a Mordell - Weil group of rank
8 of sections. By applying these sections to rational points on 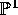 we see
that the set of rational points
we see
that the set of rational points 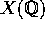 is dense in X.
is dense in X.
It is not hard to modify this example to obtain a varying family of elliptic
surfaces which has a dense collection of sections. Let B be a curve and let
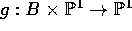 be a family of rational functions on
be a family of rational functions on 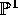 which varies in moduli (such families exists as soon as the degree is at least
3). Let Y be the pullback of X to
which varies in moduli (such families exists as soon as the degree is at least
3). Let Y be the pullback of X to 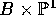 . Then
. Then 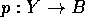 is a
family of elliptic surfaces, of variation
is a
family of elliptic surfaces, of variation 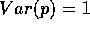 , and relative kodaira
dimension 1. By composing sections of E with g and arbitrary rational maps
, and relative kodaira
dimension 1. By composing sections of E with g and arbitrary rational maps
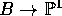 , we see that p has a dense collection of sections.
, we see that p has a dense collection of sections.
Harris's weak conjecture for elliptic surfaces is attributed to
Manin. At least over 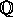 , it is closely related to a conjecture of Mazur
[Maz]. In case of surfaces over
, it is closely related to a conjecture of Mazur
[Maz]. In case of surfaces over 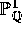 , it has been related to
the conjecture of Birch and Swinnerton-Dyer: let
, it has been related to
the conjecture of Birch and Swinnerton-Dyer: let 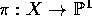 be an
elliptic surface defined over
be an
elliptic surface defined over 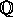 . In [Man], E. Manduchi
shows that under certain assumptions on the behavior of the j function, the
set of points in
. In [Man], E. Manduchi
shows that under certain assumptions on the behavior of the j function, the
set of points in 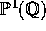 where the fiber has root number -1 is dense
(in the classical topology). According to the conjecture of Birch and
Swinnerton-Dyer, the root number gives the parity of the Mordell-Weil rank. It
is likely that some of Manduchi's conditions (at least condition (1) in Theorem
1 of [Man]) can be relaxed once one passes to a number field.
where the fiber has root number -1 is dense
(in the classical topology). According to the conjecture of Birch and
Swinnerton-Dyer, the root number gives the parity of the Mordell-Weil rank. It
is likely that some of Manduchi's conditions (at least condition (1) in Theorem
1 of [Man]) can be relaxed once one passes to a number field.
What can be said in case 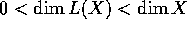 ? In [H2], Harris
proposed the
following definition:
? In [H2], Harris
proposed the
following definition:

Harris proceeded to propose the following:
I do not know whether or not Harris himself believes this conjecture. This does not really matter. What is appealing in this conjecture, apart from it's ``tightness'', is that any evidence, either for or against it, is likely to be of much interest.
For lack of any better results, we just note that proposition 1.8 directly implies the following:
ACKNOWLEDGEMENTS I would like to thank D. Bertrand, J. Harris, J. Kollár, K. Matsuki, D. Rohrlich and J. F. Voloch for discussions related to this note.


