





Proof.
Let 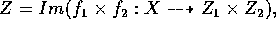 and let
and let 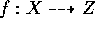 be the induced map. The map
be the induced map. The map 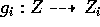 is
dominant and has irreducible general fiber. We claim that Z is a variety of
general type. If either
of
is
dominant and has irreducible general fiber. We claim that Z is a variety of
general type. If either
of 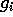 is generically finite (and therefore birational) then this is clear.
By Viehweg's additivity theorem ([V1], Satz III), it
suffices to show that the generic fiber of
is generically finite (and therefore birational) then this is clear.
By Viehweg's additivity theorem ([V1], Satz III), it
suffices to show that the generic fiber of 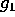 is of general type. This
follows since the fibers of
is of general type. This
follows since the fibers of 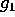 sweep
sweep 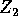 . (Specifically, let d be the
dimension of the generic fiber of
. (Specifically, let d be the
dimension of the generic fiber of 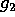 . Choose a
general codimension-d plane section
. Choose a
general codimension-d plane section  , then
, then 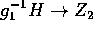 is generically finite and dominant, therefore
is generically finite and dominant, therefore 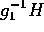 is of general type,
therefore the generic fiber of
is of general type,
therefore the generic fiber of 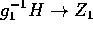 is of general type.)
is of general type.)
Proof. Given an extension 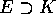 let
let 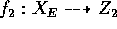 be a
dominant rational map. By the lemma above with
be a
dominant rational map. By the lemma above with 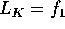 there
exists a variety Z and a dominant rational map with irreducible general fiber
there
exists a variety Z and a dominant rational map with irreducible general fiber
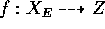 dominating both
dominating both 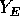 and
and 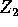 . By maximality
. By maximality 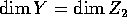 and since the general fibers of
and since the general fibers of 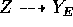 are irreducible,
are irreducible, 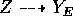 is
birational. The map
is
birational. The map 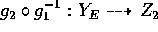 gives the required
dominant rational map.
gives the required
dominant rational map.
Proof of the theorem.
Using Stein factorization we may restrict attention
to maps with irreducible general fibers. As above, let 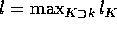 ,
and let
,
and let 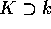 be an extension such that
be an extension such that 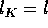 .
We need to show that
.
We need to show that  can be descended to k.
can be descended to k.
First, we may assume that
K is finitely generated over k, since both Y and 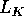 require only
finitely many coefficients in their defining equations.
require only
finitely many coefficients in their defining equations.
Next, we descend 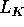 to an algebraic extension of k. Choose a model B for K, and a model
to an algebraic extension of k. Choose a model B for K, and a model
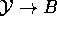 for Y. We have a dominant rational map
for Y. We have a dominant rational map  over
B. There exists a point
over
B. There exists a point 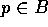 with
with  finite, such
that
finite, such
that 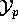 is a variety of general type of dimension l and such that the
rational map
is a variety of general type of dimension l and such that the
rational map 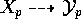 exists. The lemma above shows that
exists. The lemma above shows that 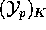 is
birational to Y. Alternatively, this step follows
since by theorems of Maehara (see
[Mor]) and Kobayashi - Ochiai (see [MD-LM]) the set of rational
maps to varieties of general type
is
birational to Y. Alternatively, this step follows
since by theorems of Maehara (see
[Mor]) and Kobayashi - Ochiai (see [MD-LM]) the set of rational
maps to varieties of general type 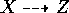 is discrete, therefore
each
is discrete, therefore
each 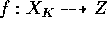 is birationally equivalent to a map defined
over a finite extension of k.
is birationally equivalent to a map defined
over a finite extension of k.
We may therefore replace K by an algebraic Galois extension of k, which we
still call K. Let 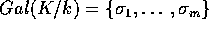 . For any
. For any 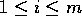 we have a rational map
we have a rational map
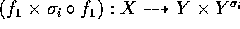 . Applying lemma
1.3 we obtain a birational map
. Applying lemma
1.3 we obtain a birational map
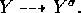 There are open sets
There are open sets 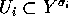 over which these
maps are regular isomorphisms, giving rise to descent data for
over which these
maps are regular isomorphisms, giving rise to descent data for  to
k.
to
k.
Is there a way to describe the fibers of the Lang map 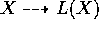 ? A first
approximation is provided by the following:
? A first
approximation is provided by the following:
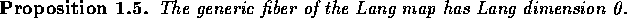
Proof. Let 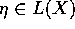 be the generic point and let
be the generic point and let 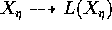 be the lang map of the generic fiber. Let
be the lang map of the generic fiber. Let 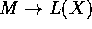 be a model of
be a model of
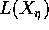 . By definition, the generic fiber
. By definition, the generic fiber 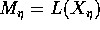 of M is of
general type, therefore by Viehweg's additivity theorem M is of general type,
and by definition M is birational to
of M is of
general type, therefore by Viehweg's additivity theorem M is of general type,
and by definition M is birational to 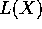 .
.
We will see that the answer is yes, if one assumes the following inspiring conjecture of higher dimensional classification theory:
This conjecture allows us to ``construct'' the Lang map ``from above'':
The proof is obvious.


