Self-Intersecting Quadrilaterals
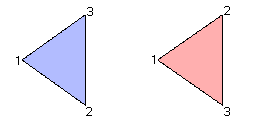
Figure 3. The triagle on the left is oriented in the counter-clockwise direction and so has positive area; the triangle on the right has negative area.
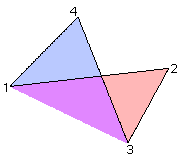
Figure 4. A self-intersecting quadrilateral
By dividing the region into two triangles along the diagonal (which lies outside the original polygon), we can easily calculate the total area of the quadrilateral. The triangle 123 has negative area, and the triangle 134 has positive area. Thus the purple region outside the quadrilateral is counted once positively and once negatively, and so does not affect our calculation, leaving us with nothing but the red and blue regions, which have the correct sign.
Once we have this decomposition, a simple adaptation of the proof for non-convex quadrilaterals shows us that the area ration for self-intersecting quadrilaterals is also 1/2.