

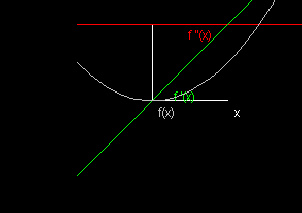
Exercises
|

Exercises
|

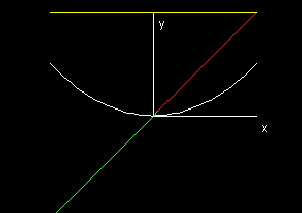
Exercises
|
Taylor series are polynomials that approximate functions. 
If we know up to the nth derivative of f(x) as
well as the function value at x0, then we can
construct a Taylor polynomial of degree n. 
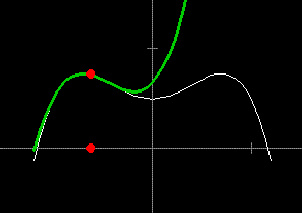
Exercises
|
|
Suppose we want to find the maximum and minimum values of some function f(x) that satisfy the condition that some function g(x) is equal to c.
If g(x) is only equal to c for a finite number of x values (which is true except for a few special cases, such as g(x) being a constant function equal to c), then the solution is simply to see which of these values of x yields the maximum and minimum values of f(x).
Exercises
|