If we wanted to find the average
position of a series of particles on an interval, we could find this
position by adding up the values of the x-coordinate from each point
(the only coordinate in one dimension) and dividing by the number of
points. This is expressed as follows:
(Σnxn)/n
Where xn is the x coordinate of the position of
the nth particle.
Suppose instead we wanted to find the center of mass of an interval
as described in the first paragraph. Our expression for the x
coordinate of the center of mass, given the mass mn
of each particle is:
(Σnxnmn)/(Σnmn)
(Note that the denominator is equal to the total mass of the set of
particles.)
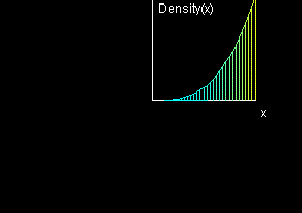
Given a linear density function ρ(x), we can express this
summation as
(Σnxn*ρ(xn)*hn)/(Σnρ(xn)*hn)
Where hn is the width of the nth particle.
For an interval with domain D composed of a very large
number of particles, we can change this summation to a double integral,
replacing hn with dx:
X = (∫Dx*ρ(x)dx)/(∫Dρ(x)dx).
This gives us the center of mass (X) of D.