Recall that the procedure for evaluating single variable integrals is to
1. Approximate the area under the graph using rectangles, and
2. Take the limit of the sum of the area of these rectangles as the
number of rectangles approaches infinity.
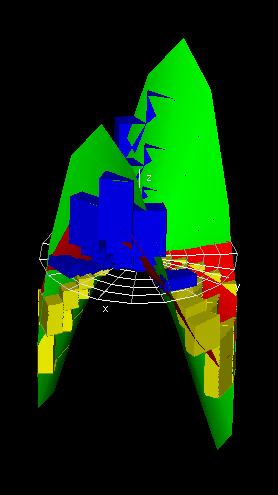
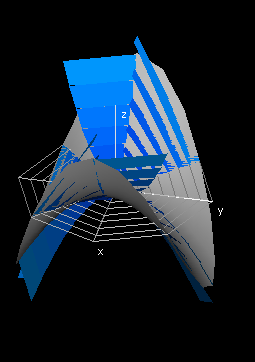
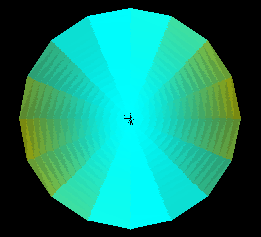
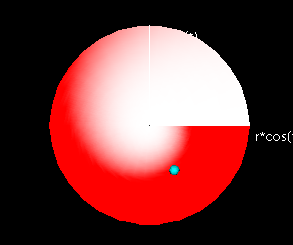
Similarly, the volume underneath the function graph for a double
integral can be found by
1. Dividing the domain R into rectangles,
2. Erecting rectangular prisms over these rectangles using the value of
the function graph at the bottom-left vertex of each rectangle as the
height,
3. Taking the limit of the sum of the prisms' volumes as the number of
rectangles in the domain aproaches infinity. 
If we apply Fubini's Theorem to integrals using polar coordinates, we get
∫ab∫cdf(x, y)rdrdθ = ∫cd∫abf(x, y)rdθdr = ∫∫Rf(r, θ)dA
Where dA = dr*dθ.
Exercises
|
|
