Vector Fields 3D
Contents
A vector field is defined by a function which associates a vector with
each point in the domain of the function. 
In two dimensions, a vector field V can be expressed in
terms of the functions p(x,y) and q(x,y) as V(x,y)
= (p(x,y),q(x,y)).
Note that for the gradient vector field, p = fx
and q = fy. 
Conservative Vector Fields 3D
Top of Page
Contents
A two-dimensional vector field F = (p(x,y),q(x,y)) is conservative
if there exists a function f(x,y) such that F = ∇f.
If f exists, then it is called the potential function of F.
If a two-dimensional vector field F(p,q) is conservative,
then py = qx. 
Suppose that F is
conservative and so there does exist a function f such that F
= ∇f. Then p = fx and q = fy.
Now consider the mixed partials fxy = py
and fyx = qx. By the equality of mixed
partials, py = fxy = fyx = qx.

Exercises
1. For each of the following, use the demo to determine
whether or not the vector field F is conservative. If it is
conservative, find the potential function of F.
- F = (x, y)
- F = ( 1, y)
- F = ( 0, -9.8)
- F = (cos(x), sin(y))
- F = (-y, x)
- F = (x/(x2+y2), y/(x2+y2))
2. Why won't the green curves necessarily lie on the graph of
f(x, y) (the function whose gradient is F) if
the blue and red paths have different starting points? (Assume F
is conservative.)
|
Circulation 3D
Top of Page
Contents
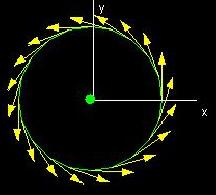
If C(t) = (x(t),y(t)), α ≤t≤β is a parametrized curve in
the plane, then the velocity vector C'(t) is given by C'(t)
= x'(t),y'(t)) with length equal to the speed = s'(t) =
√(x'(t)2 + y'(t)2). The unit tangent
vector is defined to be T(t) = C'(t)/s'(t).
If V = (p(x,y),q(x,y)) is a differentiable vector field
in the plane, then the circulation of V along C is defined to
be the integral
∫C V⋅T ds = ∫αβ
(p(x(t),y(t)),q(x(t),y(t))⋅((x'(t),y'(t))/s'(t))s'(t) dt
= ∫αβ p(x(t),y(t))x'(t) +q(x(t),y(t))y'(t) dt
= ∫C p(x,y)dx + q(x,y)dy.
Note that the circulation of ∇f(x,y) along a curve C
equals ∫ab fx(x(t),y(t))x'(t) + fy(x(t),y(t))y'(t)
dt = ∫abd/dt(f(x(t),y(t)) dt = f(x(t),y(t))|ab
= f(x(b),y(b)) - f(x(a),y(a)). In particular, if F(x,y)
is a conservative vector field then the circulation of F
along a closed curve is 0.
 [D]
[D]
Curl
Top of Page
Contents
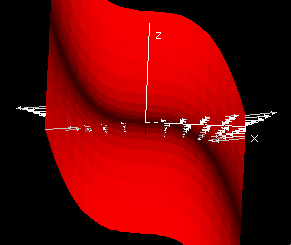
The
scalar curl of a two-dimensional vector field is defined as
scalar curl V = -py(x,y)+qx(x,y).

The curl of a vector field V
is usually defined for a vector field in three variables by the
condition curl V = ∇ x V. If the third coordinate is 0,
then curl(p(x,y),q(x,y),0) = ∇ × (p(x,y),q(x,y),0) = (0,0,qx-py).
The third coordinate, -py(x,y)+qx(x,y)
is called the scalar curl of V. The scalar curl of
a vector field in the plane is a function of x and y
and it is often useful to consider the function graph of the (x,y,-py(x,y)
+ qx(x,y)). 
If a two-dimensional vector field F(p,q) is conservative, then its curl
is identically zero.

Since py = qx,
∇ × F = (0,0,qx-py) = (0,0,0).

Flux
Top of Page
Contents
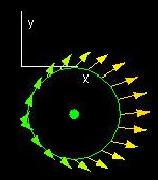
If
C(t) = (x(t),y(t)), α ≤t≤β is a parametrized curve in
the plane, then the
velocity vector C'(t) is given by
C'(t)
= x'(t),y'(t)) with length equal to the
speed = s'(t) =
√(x'(t)2 + y'(t)2)The
unit
normal vector is defined to be
N(t) = (y'(t),-x'(t))/s'(t).
If
V = (p(x,y),q(x,y)) is a differentiable vector field
in the plane, then the
flux of V across C is defined to be
the integral
∫C V⋅N ds = ∫αβ
(p(x(t),y(t)),q(x(t),y(t))⋅((y'(t),-x'(t))/s'(t)) s'(t) dt
= ∫αβ p(x(t),y(t))y'(t)
-q(x(t),y(t))x'(t) dt
= ∫C- q(x,y)dx+ p(x,y)dy
 [D]
[D]
Divergence 3D
Top of Page
Contents
The divergence of a vector field V(x,y) = (p(x,y),q(x,y))
is defined as div V = ∇ ⋅ V = px + qy.

Note that divergence of a vector
field is a scalar value.

Green's Theorem (Circulation-Curl or Tangetial Form) 3D
Top of Page
Contents
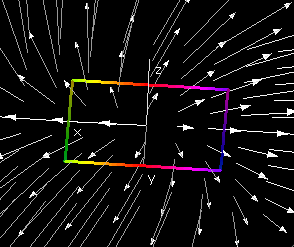
Let P(x,y) and Q(x,y) be differentiable functions
of x and y. Let D be a region in the
plane and let C be the boundary of D. The
tangential version of Green's
theorem states that
∫C P(x,y) dx + Q(x,y) dy = ∫∫D (- Py(x,
y) +Qx(x, y)) dxdy.
where D is the region in the plane bounded by the oriented
curve C
Green's Theorem (Divergence-Flux or Normal Form) 3D
Top of Page
Contents
[D]






