Animals : {Spiral Shells}

A Golden Spiral (also known as a Logarithmic Spiral) is a geometrical concept that can be derived from the Golden Rectangle.  A rectangle with side lengths in proportion to the Golden Proportion (1 to 1.618) can be divided into a square with side length 1, and the rectangle remaining will exhibit the Golden Proportion on a smaller scale; this rectangle can be divided into a square and a rectangle, and this process can continue infinitely at a smaller and smaller scale. 

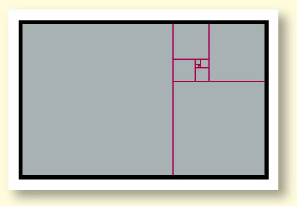
The Golden Spiral is created by drawing an arc equal to the circumference of a circle connecting the two opposing corners of each of the squares, which when connected form a spiral.  This spiral may appear familiar to us, and in fact the spirals that make up the physical structures of animals such as the nautilus and conch closely exhibit the Golden Spiral’s proportion.

A slice of a nautilus shell revealing a bisection of its many chambers reveals the Golden Proportion in a number of dimensions: the one-dimensional line of the spiral follows the form of the Golden Spiral, the length and width of the shell correspond closely to the proportions of the two-dimensional Golden Rectangle, and three-dimensionally, the ratio of the volumes of each pair of consecutive chambers is approximately 1 to 1.618.

 
 
Downwards in the tree: {Animals}


Sources: golden ratio image, <http://www.ics.uci.edu/~eppstein/junkyard/spiraltile/>; nautilus shell, <http://www.shelterpub.com/_symmetry/nautilus.gif>; conch shell, <http://www.csacourses.com/shell.jpg>. Koshy, Thomas. Sacred Geometry website, <http://www.sacredgeometry.com/golden%20ratio%20i.htm>