 |
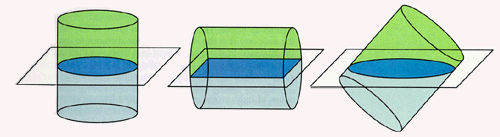
Slicing a cylinder suspended from the top (left); slicing a cylinder suspended from the side (center); slicing a cylinder suspended from the rim (right).
Friedrich Froebel's third figure was a circular cylinder. Once we understand the slicing sequences for balls and cubes, it is easy to imagine two of the sequences for the cylinder. If the cylinder is suspended from the center of its circular top, then the slices will all be circular discs. We obtain "a disc for a while," the Flatlanders' perception of a solid cylinder penetrating their world face first.
If we suspend the cylinder from the center of one side so that its circular ends are vertical, then the first slice will be a single segment, which expands to form a rectangle. The rectangle continues to expand until its side length equals the diameter of the circular disc. Then the sequence reverses and the rectangle shrinks back to a single edge.
More complicated are the slices of a cylinder suspended from a point on its rim. Half way through, the slice of the circular cylinder is an ellipse.
|
||
Slicing a cylinder suspended from the top (left); slicing a cylinder suspended from the side (center); slicing a cylinder suspended from the rim (right). |
Slicing sequences give us a way to think about an analogue of the cylinder in the fourth dimension. We can imagine a figure that in one guise would appear as "a ball for a while," and in another would appear as a segment, which expands to a thin cylinder, and continues to expand until the cylinder reaches the diameter of the ball, then shrinks back to a single segment. A "diagonal" view of the same object would have in its middle position an ellipsoid, a figure whose plane sections are all ellipses.
| Slicing Cones | ||
| Table of Contents | ||
| Slicing the Triangular Pyramid |