 |
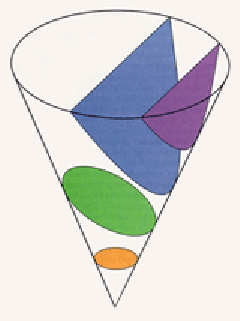
Slicing the cone to produce the conic sections. From top to bottom: hyperbola, parabola, ellipse, circle.
In the late nineteenth century, a young American draftsman and toy manufacturer, Milton Bradley, took up the task of providing geometric models for kindergartens. To Froebel's trio of sphere, cylinder, and cube, he added a cone, which could also be suspended from different eyelets. Students could imagine the slices, called conic sections, made by various horizontal planes. In presenting this object, Bradley was bringing young students into contact with a distinguished chapter in the history of solid geometry, and he was introducing them to shapes with a great many applications in the physical world.
|
||
Slicing the cone to produce the conic sections. From top to bottom: hyperbola, parabola, ellipse, circle. |
Apollonius of Perga recognized a fundamental fact that links the second and third dimensions: the ellipse, the parabola, and the hyperbola can all be obtained by slicing a cone in ordinary space. These curves were already important in optics because they gave the shapes of lenses. Geometers knew how to describe these curves as the solutions of locus problems. A parabola was the collection of points whose distance to a given focus point was equal to the distance to a line lying outside the parabola, called the directrix. When the distance from each point to the focus was one-half the distance to the directrix, the collection of points formed an ellipse. The same name was given to any curve having the property that the ratio between the distance to the focus and the distance to the directrix was less than one ("ellipse" means "falls short"). A curve having a ratio that is greater than one yields a hyperbola.
We see conic sections frequently, for example in the solid cones of light ascending and descending from a lampshade. The boundary of this double solid cone determines the edge of the shadow on any wall in the path of the light. The wall slices the light cone and gives us a conic section.
If we hold a flat plane directly over the shade, we get a circle, growing larger and larger as we move the plane farther and farther away. If we tilt the plane slowly, the circle of light becomes an ellipse, and moving the plane farther away produces a larger ellipse (having the same ratio between the largest and smallest axis). Tilting farther gives ellipses with greater and greater elongations until finally, as the plane becomes parallel to one of the rays coming past the edge of the shade, the conic section is no longer an ellipse but a parabola, stretching out to infinity.
When we look at a shadow cast by a lampshade, most of the time we observe neither an ellipse nor a parabola. A vertical wall placed next to the lamp cuts out the two branches of a hyperbola, both stretching out to infinity. Frequently the lower and the upper branch are not part of the same hyperbola since the position of the bulb or the slant of the sides of the shade might create an upper cone that does not match the lower cone. If we center a bulb halfway up a cylindrical lampshade, then a vertical wall will slice the light cone to form a complete hyperbola, in theory anyway.
There is a difference between the mathematical discussion and the physical observations that inspired it. In reality a light bulb is not a point source of light, and the edge of a shadow will never be a precise curve. As the slicing plane moves away from the bulb, the image becomes more and more diffuse. To say that an image is a circle or an ellipse is already a mathematical abstraction. To say that an image is a parabola is a much greater abstraction. No matter how intensely the beam were focused, it would take forever to trace out the whole parabola. After all, the beam takes a year to travel just one light-year. Nonetheless, we state without fear of contradiction that in the ideal order the slice of a perfect cone by a perfectly flat plane parallel to one of the lines of the cone will be a perfect parabola. The applications of this to optics, or to planetary motion, are the provinces of physicists and astronomers.
A comet on an elliptical orbit about the sun, such as Halley's comet, will return to our solar system again and again at regular intervals. A comet on a parabolic or hyperbolic orbit will eventually move farther and farther from the sun, finally vanishing from sight never to appear again. After a few observations an astronomer might be able to tell what sort of orbit a given comet is following, although sometimes that is a very delicate proposition. When a comet is on a nearly parabolic path, it is very difficult to tell whether it is on an elliptical path and will return after a great amount of time or on a hyperbolic path with no possible return. Often the shape of the orbit is simply "too close to call."
| Contour Lines and Contour Surfaces | ||
| Table of Contents | ||
| Slicing Cylinders |