The Greeks set up a particularly challenging set of rules when they formalized their notions of geometry. They restricted the set of tools that could be used for constructing figures to two instruments: a straightedge (with no markings on it) and a compass. The straightedge enabled geometers to draw a line through any two points, and the compass enabled them to draw a circle that had a given point as center and that passed through another given point.

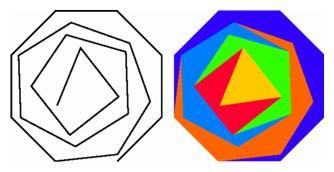
	A computer graphics re-creation of the first 2 of 16 versions of a polygonal progression designed by the Swiss artist Max Bill in 1938. The equal-sided polygons progress outward from the center, from a three-sided polygon at the heart to an eight-sided polygon on the outer edge.

For the Greeks, as well as for today's geometers, a polygon was a plane figure bounded by a finite number of line segments, and a regular polygon had all side lengths equal and all angles equal. Furthermore, the Greeks required that a polygon not intersect itself and that all its diagonals should lie inside the figure. In order to construct a regular polygon having a certain number of edges, it is necessary to subdivide the circumference of a circle into a number of arcs of equal length. In certain cases, this is easy to do using only a straightedge and compass. In other cases, this construction is somewhat more involved, and in still others, it is completely impossible.

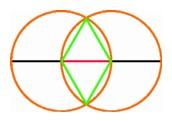
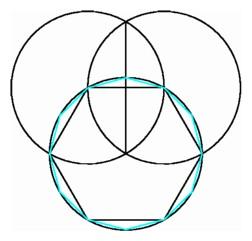
The first theorem in Euclid's Elements, the most famous textbook of all time, provides a method for constructing a regular triangle. We start with a red segment for one side of the triangle and use a compass to describe two orange circles, each with one endpoint of the segment as a center and the other endpoint on the circumference. These two circles meet at two points, and each of these points is the third vertex of a green equilateral triangle having the given segment as base.

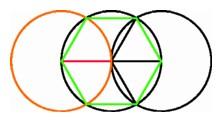
We can then extend the red base to intersect the left circle at another point, and from this point as center, we describe a third orange circle of the same radius, meeting the middle circle in two additional points. In this way we obtain six equally spaced points on a circle, forming the vertices of a green regular hexagon. By taking every second vertex as we go around, we divide the circumference into three equal parts, giving the vertices of a blue regular triangle inscribed in the middle circle.

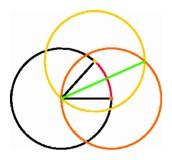
	The first theorem in Euclid's Elements, the construction of the equilateral triangle (left); Construction of the regular hexagon inscribed in a circle (center); Euclid's argument for bisecting an angle (right).

Once we have a regular polygon of a certain number of sides, it is easy to construct one with twice the number of sides just by bisecting each arc using the straightedge and compass. We draw two full circles, orange and yellow, each having an endpoint of the red arc as its center and passing through the original center. These circles meet at two points, the original center and a new point. If we connect these points with the straightedge, the new green line intersects the original red arc in its midpoint.

By bisecting the six sides of the regular hexagon we obtain 12 points equally spaced on the circle. These points are the vertices of a blue regular dodecagon. Similarly, we obtain a regular polygon with 24 sides, or 48, or an arbitrarily large number, simply by dividing the sides of a polygon in half over and over again. Thus the number of regular polygons that can be constructed just using a straightedge and a compass is unlimited. We can state this more emphatically: there are infinitely many regular polygons in the plane.

In this sentence the words "there are" say something extremely important about the nature of mathematical objects. No one has ever seen a perfect regular triangle, although we have a procedure for generating a representation of one that is as close to perfect as we wish. The concept of "regular triangle" or "regular polygon with four or five or seven sides" makes sense. Such objects have an abstract existence, whether or not anyone ever tried to draw one. We do not know if anyone, using any method whatsoever, has ever constructed a regular polygon with 3072 sides, but we know it can be done and we know how to do it, by starting with the regular triangle and applying the bisection procedure ten times.

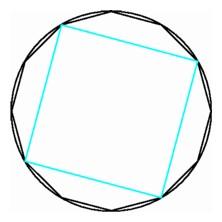
	Using bisection to construct the regular dodecagon (left); A square inscribed in a dodecagon (right).

We can easily construct other familiar regular polygons, like the square, once we know how to erect a perpendicular to a line from a point on the line. Or we can find a square inscribed in a given circle by joining every third vertex of a regular dodecagon. Once we have the square, we can use bisection to get an entirely new infinite family of regular polygons with 8 sides, 16 sides, and so on, for any power of two.

These relatively easy methods provided constructions for the regular polygons with three, four, six, and eight sides. What about five, seven, and nine? The Greeks solved the problem for a regular pentagon by means of a clever construction related to the geometric solution of a quadratic equation. But no matter how hard they tried, they were unable to construct the regular heptagon with seven sides or the regular enneagon (or nonagon) with nine sides.

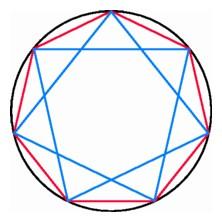
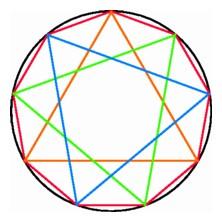
	Connecting the diagonals of a heptagon forms a heptagonal star (left); three triangles inscribed in an enneagon (right).

It is important to distinguish between an approximate solution and an exact one. The insignia of the Los Angeles Police Department is a seven-pointed star connecting seven equally spaced points on a circle. It is possible to find the location of such points up to any desired degree of accuracy by trial and error, but it is not possible to find the points exactly, as we did for the triangle, square, and hexagon, using just straightedge and compass. Many people who proposed solutions to this problem, including some philosophers and amateur mathematicians, simply did not understand the difference between an approximation and an exact solution.

It was especially embarrassing for the Greeks that their favorite geometrical methods were unable to provide a construction for the regular enneagon. Greek geometers had already divided the circumference into three equal arcs. Now all they had to do was divide each of these arcs into three equal pieces. Dividing the segment across the arc into three equal parts and extending rays through these points does not work since the middle arc will be larger than the other two.

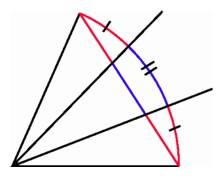
Even though there is a straightedge-and-compass method for bisecting an arbitrary angle, there is no such method for trisecting an arbitrary angle. In fact there is no possible straightedge-and-compass method for trisecting the particular angle that is one-third of a circumference, or 120 degrees. When a hopeful amateur submits a "solution" to the trisection problem, a flaw in the argument usually shows up when the proposed method is applied to this particular angle. (This does not necessarily dissuade the would-be solver.)

	Trisecting a chord does not produce a trisection of an angle.

Not until the early part of the nineteenth century did mathematicians develop the algebra that proved the impossibility of trisecting the 120-degree angle. The straightedge-and-compass method for bisecting an angle involves finding intersections of circles, and there is a corresponding algebraic process, which involves taking square roots and solving quadratic equations. The geometric problem of trisecting an angle corresponds to the algebraic problem of solving a cubic equation, and as mathematicians discovered, the straightedge and compass cannot provide the solutions of all such equations. For the 120-degree angle, the argument involves a trigonometric identity that gives the relation between the cosine of an angle and the cosine of one-third of the angle. Finding the cosine of the 40-degree angle is equivalent to solving the cubic equation 8x³ - 6x + 1 = 0, and this cubic equation cannot be solved just by taking repeated square roots.

Does that mean that the nine-sided regular polygon does not exist? Not at all. It exists just as much as a triangle or a square or a circle exists, but it cannot be constructed with straightedge and compass, so we cannot expect to encounter it among the objects of Euclid's plane geometry. Existence is not the same as constructibility. There exist infinitely many different regular polygons, one for each number greater than two, even though we can't construct them all using the classical Greek methods.

			The Search for Regular Polyhedra
			Table of Contents
			Introduction