 |
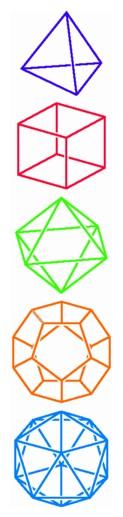
The five regular polyhedra in three-space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
In contrast with the unlimited number of regular figures in the plane, the number of regular objects in three-space is small. The Greek geometers not only found them all, they also proved that there weren't any more to be found.
| ||
The five regular polyhedra in three-space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. |
Long before Greek mathematicians formalized the axioms for solid geometry, people were familiar with several regular polyhedra, in particular the cube, the tetrahedron (the Greek term for a figure with four faces), and the octahedron (a figure with eight faces formed by putting together two square-based pyramids with equilateral sides). If we wished to follow the Greek usage completely, we should call the cube a hexahedron, but we will continue to use the familiar Latin expression. The cube has three squares at each vertex, the tetrahedron has three equilateral triangles at each vertex, and the octahedron has four equilateral triangles at each vertex. All the faces of a regular polyhedron must be regular polygons, and there must be the same number of faces meeting at each vertex. Do any other solid figures satisfy these requirements?
By the time Euclid wrote his textbook, two more regular polyhedra had been discovered. In the thirteenth and final book of his Elements, Euclid included a proof that there could not be more than five regular polyhedra. It is worth our while to consider the proof carefully because it contains an idea that can assist us when we ask how many regular figures exist in higher dimensions.
Euclid first observed that for a regular polyhedron the angles that come together at a given vertex add up to less than 360 degrees. For example, the three squares at a vertex of a cube have an angle sum at the vertex equal to three right angles, or 270 degrees. Next he noted that in order to make a polyhedron, at least three faces must meet at each vertex. If we want to make a regular polyhedron with triangular faces, we then have only three possibilities: three, four, or five triangles at each vertex. Six triangles will already fill the area around a point, leaving no gap that would allow us to fold the object up in three-space.
| ||
Possible arrangements of triangles around a point in the plane. |
Three triangles meeting at a vertex fold into a triangular pyramid, and adding one more face gives the tetrahedron. Four triangles meeting at a vertex fold into a pyramid with a square base, and putting two of these pyramids together along a common square face gives the octahedron. Five triangles meeting it a vertex fold into a pentagonal pyramid with a regular pentagon as base and five equilateral triangles as sides. To construct a regular polyhedron that includes this figure, we begin with a strip of 10 equilateral triangles alternately pointing up and down and two regular pentagons with the same side length. By fitting these pieces together, we construct a pentagonal antiprism: one regular pentagon is the base; the other regular pentagon, slightly rotated, is the top; and the strip of triangles is sandwiched between such that each edge of a pentagon is an edge of an equilateral triangle having its third vertex on the other pentagon. We then erect pentagonal pyramids on the top and bottom pentagons to obtain a figure with 20 equilateral triangles, called a regular icosahedron.
This completes the list of regular polyhedra with triangular faces, but what about other regular polygons? It is possible to fit three squares around a point, but four already fill the area around a point, so the cube is the only regular polyhedron with square faces. We will not find any regular polyhedron with hexagonal faces since three hexagons already fill the area around a point. Three polygons with more than six sides will more than fill the space around a point.
| |||
A pentagonal antiprism and the completed icosahedron (left); three pentagons around a point in the plane (right). |
The only candidate left is the regular pentagon. Since the angles of a pentagon are less than those of a hexagon, three pentagons will fit around a point in the plane with room left over. Since the angles of a regular pentagon are greater than those of a square, we cannot fit four regular pentagons around a point in the plane. This leaves open the possibility of a fifth regular polyhedron having three regular pentagons around every vertex. Well before the time of Euclid, Greek geometers had found this fifth regular polyhedron, a regular dodecahedron having 12 pentagonal faces.
| Duals of Regular Polyhedra | ||
| Table of Contents | ||
| The Greek Geometry Game |