 |
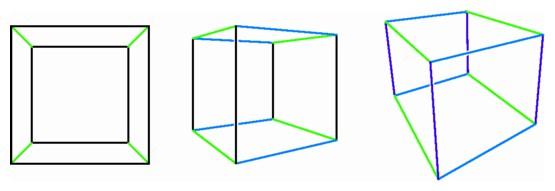
A view of a cube with one vanishing point (left); a view of a cube with two vanishing points (center); a view of a cube with three vanishing points (right).
Dalí's design relied on his mastery of perspective, one of the most useful means of interpreting visual imagery. As we stand in a doorway and look into a room, the way we see the interior furnishings depends very much on our specific viewpoint. If someone wanted to trick us, he could photograph the interior from exactly the same viewpoint and mount the life-size image on a flat screen just inside the room. If we came to the doorway and looked in again, we would see precisely what we had seen before--we would receive exactly the same visual information. How could we tell the difference between the picture and the reality?
The most natural way to tell the difference is to change the viewpoint. Coming a bit closer or moving to the side, you would see how the image shifted. A flat picture will shift quite a bit differently from a real three-dimensional room. In the real room, a square picture frame will begin to look like a trapezoid as we change our position, but in a two-dimensional picture, it will not undergo any such distortion.
We can imagine A Square doing the same thing, walking around in his space to determine whether some image he sees is a real view of a house, or merely a representation of the interior of a house painted on a one-dimensional screen. The trompe l'oeil effect should be strong in every dimension, as we can all be fooled by the illusions appropriate to our own space. If we can learn to deal with the illusions of perspective, we can use them to good advantage to help us understand complicated three-dimensional structures, and eventually to visualize objects from the fourth dimension.
Up to this time all of our images of the cube and hypercube have been shadows cast by parallel rays of light. The images of parallel lines appeared as parallel lines (or points), and parallel segments of the same length had images that were segments of the same length. We know, however, that this is not what we actually see when we take in a large view. Parallel railroad tracks seem to converge to a point on the horizon. The railroad ties may appear to be parallel to the horizon, but they get shorter and closer together as they recede into the distance. The reason why a faraway railroad tie looks smaller is that the rays from its endpoint to the observer's eye form a smaller angle than do the rays of an equal-length tie that is closer to the viewing point. In a perspective drawing, any collection of parallel lines will appear either as parallel lines or as lines converging to a vanishing point. A cube has three sets of parallel edges, and the image can have one, two, or three vanishing points.
When we look at a cube, the closer parts will have larger images and the parts farther away will have smaller ones. The front face of a cube viewed head on will be larger than the back face. This "square-within-a-square" is a familiar representation of our view of a cube from in front of one face. Images of vertical and horizontal edges appear as vertical or horizontal segments, but the edges heading away from us appear to converge toward the center. The closest and farthest faces appear to be squares, and the images of the other four faces are trapezoids. From experience we know that the six faces of the cube are squares of the same size and shape, even though they do not appear that way in any single view.
| ||
A view of a cube with one vanishing point (left); a view of a cube with two vanishing points (center); a view of a cube with three vanishing points (right). |
To get a better picture of the cube, we could look at a whole sequence of views as we walk around the cube, or, equivalently, as we stand still and the cube spins about a vertical axis. As the cube begins to spin, the images of vertical lines remain vertical, but the previously horizontal and parallel segments now have images lying in lines that converge to a point. At this stage, the images of the top and bottom squares are not even trapezoids since no two edges have parallel images.
| ||
Perspective views of a cube rotating about a vertical axis. |
As the cube continues to rotate, the trapezoidal image of one of the vertical faces appears to flatten out into a vertical segment and then to open again into a trapezoid. The image appears to pass through itself as the inner and outer squares change places. The same phenomenon occurs if we rotate the cube about a horizontal axis.
Perspective always causes some distortion, but we are able to accommodate the distortions by relying subconsciously on our experiences of viewing objects. When we see a rotating cube, we think about a cube, not the varying sequence of squares, trapezoids, and more complicated four-sided figures. The more aware we become of the way we visualize shapes in three-space, the better we can apply the principles of perspective to help us visualize shapes in spaces of dimensions four and higher.
| Perspective Views of the Hypercube | ||
| Table of Contents | ||
| Introduction |