 |
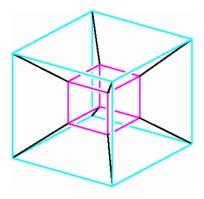
The central projection of a hypercube from four-space to three-space appears as a cube within a cube.
Analogous to the perspective views of a cube, we can imagine a sequence of perspective views of a hypercube in three-dimensional space. Just as a cube appears to be a square within a square when viewed from directly in front, the head-on view of the hypercube will appear to be a cube within a cube. The closest part of the hypercube will appear as a large cube, and the part farthest away will appear to be a smaller cube inside the larger one. In the three-dimensional case, the images of four edges of the cube join vertices of the outer square to corresponding vertices of the inner square to form four trapezoids. In the four-dimensional case, the images of eight edges of the hypercube will join vertices of the outer cube to corresponding vertices of the inner cube, thus forming six incomplete pyramids.
| ||
The central projection of a hypercube from four-space to three-space appears as a cube within a cube. |
This central projection is one of the most popular representations of the hypercube. It is described in Madeleine L'Engle's novel A Wrinkle in Time and in Robert Heinlein's classic short story ``. . . and He Built a Crooked House.'' Some writers refer to this central projection by the name tesseract, a term apparently going back to a contemporary of Abbott, C. H. Hinton, who wrote an article ``What Is the Fourth Dimension?'' in 1880 and his own two-dimensional allegory, An Episode of Flatland, the same year that Abbott wrote Flatland. The sculptor Attilio Pierelli used this projection as the basis of his stainless steel ``Ipercubo.''
Difficult as it is to imagine the perspective views of a slightly rotated three-dimensional cube, it is even more difficult to imagine the views of a hypercube as it spins in four-dimensional space. Fortunately the computer, which provided the parallel projections of the hypercube studied in Chapter 4, can also produce perspective views of the hypercube from any viewpoint we choose. The method by which it achieves this result is called central projection.
If we want to make a picture re-creating the perspective view of a cubical framework viewed from the top, we can shine a bright light from our viewing point and capture the shadow on a photographic plate below. That shadow gives an accurate record of exactly what would be seen from the viewpoint at which the picture was taken, and if we stand in that spot and look at the shadow image, we would receive the same impression as we would get from looking at the actual object.
It is not difficult to instruct a computer to make such images on a graphics screen. Once we choose a viewing point and a projection plane, the machine can determine the position of the image of a vertex by figuring out where the ray from the viewpoint through the vertex strikes the plane. Almost the same mathematics that creates a central projection of a cube on the plane can be used to create a central projection of a hypercube in three-space, and then to show the projection on the computer screen. Before we discuss the problems of visualizing the three-dimensional shadows of four-dimensional objects, we will consider the application of central projection to other figures in three-dimensional space.
See also Orthographic Views of the Cube and Hypercube| Schlegel Diagrams of Polyhedra | ||
| Table of Contents | ||
| Viewing in Perspective |