 |
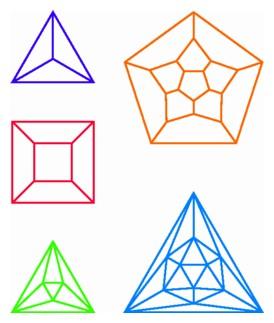
Schlegel diagrams in the plane for the five regular polyhedra: (clockwise, beginning in upper left) the tetrahedron, dodecahedron, icosahedron, octahedron, and cube.
The central projections of regular polyhedra form beautiful patterns which reveal the structure and symmetries of these objects. If a regular polyhedron has all of its vertices on a sphere in three-space, then we may use central projection from the north pole to obtain an image on the horizontal plane at the south pole. For any vertex not lying at the north pole, the line from the north pole through the vertex meets the horizontal plane at the image of the vertex. If two vertices are connected by an edge in the polyhedron, then the image of the edge is the segment in the plane joining the images of the two vertices. The images of the edges of a polyhedron are said to form a Schlegel diagram of the polyhedron, named for Viktor Schlegel, the German mathematician who invented this type of diagram in 1883. Each polyhedron has many different kinds of images formed by central projection from the north pole, depending on how the polyhedron is rotated within the sphere. We will consider only Schlegel diagrams having a special property, namely that the image of the face closest to the north pole contains the images of all the other vertices.
| ||
Schlegel diagrams in the plane for the five regular polyhedra: (clockwise, beginning in upper left) the tetrahedron, dodecahedron, icosahedron, octahedron, and cube. |
The Schlegel diagram of the cube is the familiar "square-within-a-square." For a tetrahedron, the Schlegel diagram is a triangle with its vertices connected to its midpoint. To position an octahedron for its Schlegel diagram, we rotate the polyhedron so that two of the triangular faces are horizontal. In the resulting projection, the image of the top face is a large equilateral triangle, and the image of the bottom face is a smaller equilateral triangle rotated by a half turn. The images of the other six triangles of the octahedron are triangles in the plane, each joining an edge of the inner triangle to a vertex of the outer one or vice versa. In the corresponding diagram for an icosahedron, the 12 vertices are arranged in three nested polygons: a large equilateral triangle contains a regular hexagon, which in turn contains a small equilateral triangle. The Schlegel diagram of a dodecahedron has 20 vertices similarly arranged in three nested polygons : a large regular pentagon contains a nonconvex 10-sided polygon, which in turn contains a small regular pentagon. These Schlegel diagrams display in a nice way the symmetries of the regular polyhedra and their faces.
| Schlegel Polyhedra for Regular Polytopes | ||
| Table of Contents | ||
| Perspective Views of the Hypercube |