|
Derivative Test
Text The sign of the second derivative can help determine whether a critical point is a maximum or a minimum.
If f'(x0) = 0 and f''(x0) > 0, then the function graph is convex upward at that point and the point must be a relative minimum.
Similarly if f'(x0) = 0 and f''(x0) < 0, then the function graph is convex downward at that point and the point must be a relative maximum. If f'(x0 = 0 and f''(x0) = 0, then this test is inconclusive. If f''(x0) > 0 on one side of x0 in a neighborhood of x0 and f''(x0) < 0 on the other side, then x0 is called a horizontal inflection point.
Demos
Derivative Test
| 
|
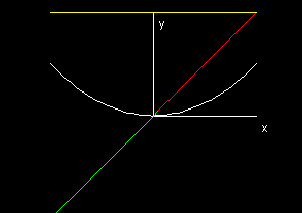
This demo displays three curves. The first, in gray, is a graph of the function f(x). The second graphs f '(x) and is red when f(x) is increasing and green when f(x) is decreasing. The third graphs f ''(x) and is magenta when f(x) is concave downward and yellow when f ''(x) when f(x) is concave upward. Notice what happens to each of these functions at maxima, minima, and inflection points.
|
Exercises 1. Use the second derivative test to determine whether each of the following critical points is a maximum or a minimum, and check using the demo:
- f(x) = x2, x = 0
- f(x) = x2 - x4, x = 0
- f(x) = x3 - 3x, x = 1
- f(x) = ex - x, x = 0
- f(x) = 1/x2 + x, x = 4√2
2. Describe what the graphs of the function, derivative, and second derivative look like at local maxima. What about local minima?
|