« Course List

MA35 Labs

1 » Single Variable Calculus

2 Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

1.1 Functions of One Variable

1.2 Differentiation

1.3 More Derivatives

1.4 Integration

1.4.1 Area under a Function Graph

1.4.2 Riemann Integral

1.4.3 Area between Function Graphs

1.4.4 Arc Length for Function Graphs

1.4.5 Change of Variables

1.4.6 Total Mass of an Interval

1.4.7 Center of Mass

1.5 Fundamental Theorem of Calculus

Search

Total Mass of an Interval

Text

The mass of a one-dimensional object is calculated by integrating its density function over the interval of the domain that it occupies. For a density function ρ(x) of one variables and an object in the domain of ρ occupying a region R, the mass is

∫_Rρ(x)dx.

Demos

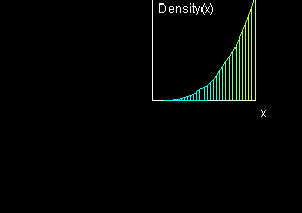
Total Mass of an Interval
	The "Density: rho(x)" window shows the density as a color gradient, where cyan indicates rho=0, yellow rho=1, and red rho=2. The "Mass" window illustrates the mass of the object as the area underneath the function graph of the density function rho.

Exercises