|
Total Mass of a Region in 3-Space
Text In order to understand how integration works in 3-space, consider the problem of finding the total mass of some region.
If we know density as a function f of x, y, and z, then we can approximate the mass of a tiny box of volume dV located at (x0, y0, z0) as the product f(x0, y0, z0)dV. We can then find the total mass by adding up these the masses of these tiny volumes.
If all three dimensions of the volumes approach 0, the summation becomes a triple integral.
Demos
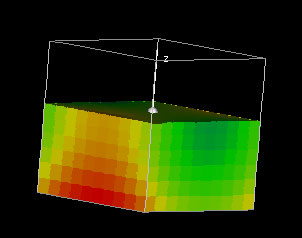
Total Mass of a Cubical Region

| 
|
This demo shows a density function f(x,y,z) over the domain -1 {leq} x, y, z {leq} 1 and computes the total mass over the domain. The function f is initially set to f(x,y,z) = x2 - y2 + z2. 
|
Exercises How could the total mass method be used as a way to understand integration for functions of one or two variables?
|