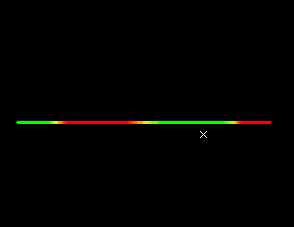Linear Functions 2D
3D Tutorial
Contents
Calculus is the study of functions. 
In
the study of functions of
one variable, we encounter domains and ranges of functions, function
graphs, and properties of functions such as continuity. In this section
introducing the study of functions of one variable, we will consider
domains and ranges of functions, function graphs, and properties of
functions such as continuity.
The simplest functions are constant functions and linear functions.

Examples
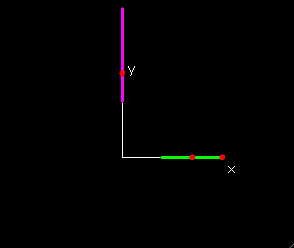
Zero Functions 
The simplest function of all is the zero function,
defined by f(x) = 0 for all x. This function can be
defined for any domain, and the range will
always always be the single point {0}. 
Constant Functions 
The next simplest class of functions are the constant functions
defined by f(x) = k for all x. A constant function
can be defined for any domain, and the range will always always be the
single point {k}. 
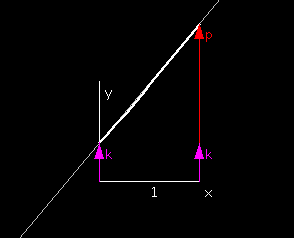
Linear Functions 
Linear functions are the next simplest class of functions,
defined
by L(x) = px + k. The number p is called the slope
of the linear function and k is called its y-intercept.
The natural domain of the linear function is all real numbers x.
If p ≠ 0, then the range of L is all real numbers.

Demos
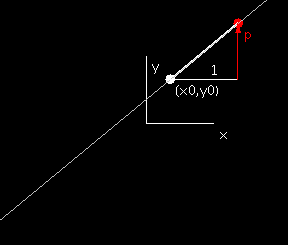
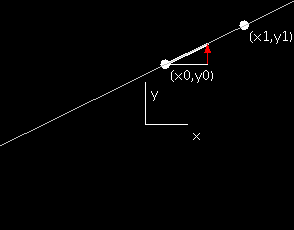
When we describe a line as the graph of a linear function f(x) = px +
k, we are giving a special role to the origin. Often it is more
convenient to consider lines through a particular point (x0,y0)
in the
plane, and we can describe such a line with slope p by the condition
(y-y0)/(x-x0) = p, so y-y0 = p(x-x0).
Choosing different values
of the slope p, we obtain all straight lines through (x0,y0)
except for
the vertical line x = x0.
Exercises
|
1. Find the segment joining the x- and y-intercepts
for y = px + k. Describe the segment.
2. Show that if p ≠ 0, then for every y
there is a point x such that L(x) = px + k = y
|
Domain, Range & Function
Graphs 2D
3D
Parametric
Equations Top of Page Contents
One-Variable Calculus considers functions of one real variable.

A
function f of one real
variable assigns a real number f(x) to each real number x
in the domain of the function. 
The domain of a function
of
one variable is a subset of
the
real line { x | x ∈ {R} }. 
The
most common domains are intervals
of the form a
≤ x ≤ b. Another common domain is an interval centered around a
point x0 with radius δ given by x0
- δ ≤ x ≤
x0 + δ. 
The range of a real-valued function f is the
collection of all real numbers f(x) where x is in
the domain of f. 
The
simplest example of a function
is the constant function
that assigns the real number k to all x in the
domain. The range of this function is the set {k}
containing one point. The next simplest example is a linear
function defined by the formula f(x) = px + k where p
is the slope of the linear function and k denotes its
y-intercept. The range of this function will be all real numbers
if p is not equal to 0 and just the value {k} if p
= 0. 
The graph of a function of one variable is the
collection of points (x,f(x)) in the coordinate plane where x
is in the domain of f. 
The
graph of a linear function of
one real variable is a line
in the coordinate plane. 
Demos
Exercises
|
1. What is the range of the function f(x) = ax2?
(The answer will depend on the constant a.)
2. What is the range of the function f(x) = -x4
+ 2x2?
|
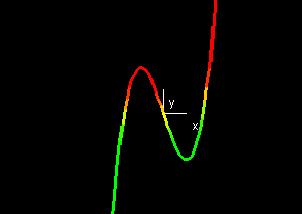
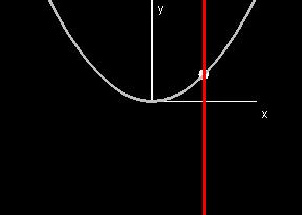
Slices
2D 3D Top of Page Contents
For every point x0
in the domain
of a function f, the
intersection of the graph of f
with the vertical line x = x0
will be the single
point (x0,f(x0)).
[D]
Exercises
|
What would happen if we
sliced a function graph in the plane with a line that wasn't vertical?
Would the slice still always be a single point? Give a proof or a
counterexample.
|
Level Sets & Contours 2D
3D Parametric
Equations
Top of Page
Contents
The collection of all points x in the domain of a function
f for which f(x) = k is called the level set of f
at level k. 
The
level set of f is
empty if there is no point x in the domain of f for
which f(x) = k. 
The set of points (x,f(x)) in the graph such that f(x)
= k is
called the contour of f at height k.
A Domain Color Graph in 1D
2D 3D Top of Page Contents
[D]
Exercises
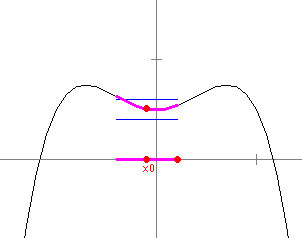
1. Find the points in the level set for each of the
following:
- f(x) = x, k = 0
- f(x) = x2 - 1, k = 0
- f(x) = sin(x), k = √2/2
- f(x) = tan(x), k = 1
2. Given a function f(x) with level set A
at k = 0 and a function g(x) with level set B
at k = 0, what is the level set of the function fg(x)
(equal to f(x) * g(x)) at k = 0?
|
Continuity
2D
3D Parametric Equations
Top of Page
Contents
One of the most important
properties of functions of one real variable is continuity.
The basic intuition for continuity is that the range of a function f(x)
will lie in an arbitrarily small interval centered at f(x0)
if x is restricted to lie in a sufficiently small interval centered at x0. Geometrically, this means
that the graph of f(x) will lie between a pair of parallel lines y = f(x0) – ε and y = f(x0) + ε, i.e. f(x0) – ε < f(x) < f(x0) + ε if x is required to lie in the
interval (x0 – δ, x0+ δ), i.e. . – δ < x-x0 < – δ.
According to the epsilon-delta definition, a function f of one real
variable is said to be continuous
at x0 if for any ε > 0 there exists a
δ such that | f(x) - f(x0) | < ε whenever |x – x0 | < δ.
A function f of one real variable is said to be continuous if it is continuous at
all points x0 in its domain.
Exercises
|
1. Consider the function f(x) = (x - 1)2
for x ≠ 1 and f(1) = 2. Why is this function not
continuous at x = 1? What if f(1) = k for some
other constant?
2. Consider the function f(x) = tan(x - 1) for x
≠ 1 and f(1) = 2. Why is this function not continuous at
x = 1? What if f(1) = k for some other
constant?
3. Consider the function f(x) = sin(1/(x-1)) for x
≠ 1 and f(1) = 2. Why is this function not continuous at
x = 1? What if f(1) = k for some other
constant?
|