Derivative of Functions of Two Variables in Polar Coordinates 1D3DContents
A function f[r,θ]=f(rcos(θ), rsin(θ)) (alternatively f(x,y)=f[ √(x2+y2)2,
tan-1(y/x)]) is differentiable
at a point (r0,θ0)
if there is a
well-defined tangent plane at the point (r0,θ0,f[r0,θ0]),
i.e. if there is a
plane L(r,θ) = p(r-r0) + q(θ-θ0) + f[r0,θ0]
which is closer to the
graph than any other plane through the point.
At the end of
Section 2, we will develop formal criteria for differentiability, and
in the meantime, we will investigate properties that a tangent plane
must have.
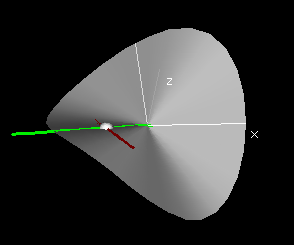
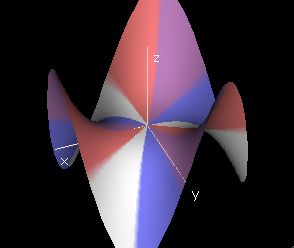
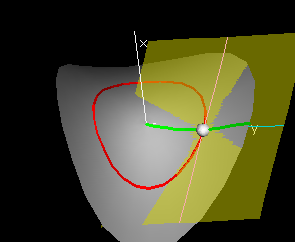
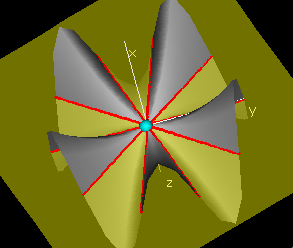
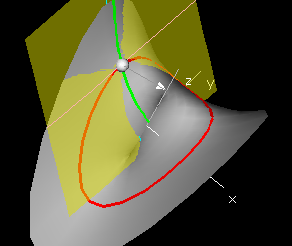
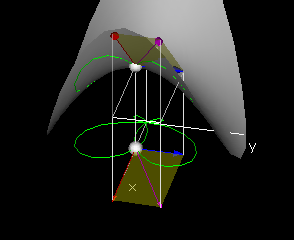
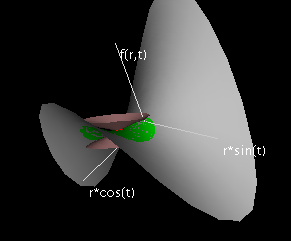
If there is a well-defined best-approximating plane, then the
intersection of that plane with a vertical plane over a line in the
domain will be a line which is the tangent line to the slice curve over
the line. In particular, for the slice curve (r,θ0,f[r,θ0]),
the
tangent line will lie in the tangent plane, if such a plane
exists. The slope of this tangent line is called the r-partial
derivative of f at (r0,θ0).
Then the r-slope p of the linear function is called the r-derivative
of f at (r0,θ0), denoted fr[r0,θ0]
and the θ-slope q is called the θ-derivative
of f at (r0,θ0) denoted fθ[r0,θ0].
The partial derivatives of a function of two variables in polar
coordinates are the slopes
of the slice curves with respect to r, and θ.
If
f[r,θ]
is
a polar coordinate function
of two variables, then for each θ = θ0,
the function f[r,θ0]
is a differentiable function of r, and its derivative is
denoted fr[r0,θ0],
called the first partial derivative of f with respect to r.
Similarly the derivative of the r = r0 slice
curve f[r0,θ]
with respect to θ is denoted
by fθ[r0,θ0],
called the first partial derivative of f with respect to
θ.
A critical point of a function of two variables f[r,θ] is a point [r0,θ0]
such that fr[r0,θ0] = 0 and fθ[r0,θ0]
= 0.
If there is a tangent plane at such a point, then the
tangent plane is horizontal.
The r-partial derivative of the
function f is itself a function fr defined over the
same domain as f. The collection of points [r,θ] in the domain
such that fr[r,θ] = 0 will be the fold set in the r-direction.
Similarly the fold set in the
θ-direction is the collection of points for which fθ[r,θ]
= 0. The critical points occur at the intersection of the fold
set in the r-direction and the fold set in the θ-direction.
For functions of two variables in polar coordinates, there is more than
one form of the
chain rule.
The first example comes when f[r,θ] is a function of
two variables, each of which is a function of t. We then get z(t)
= f[r(t),θ(t)] and z’(t) = fr[r(t),θ(t)]r’(t) + fθ[r(t),θ(t)]θ’(t).
The curve (r(t),θ(t),z(t)) has tangent vector (r’(t),θ’(t),z’(t)) lying
in the tangent plane to the graph z = f[r,θ], and this vector projects
to the vector (r’(t),θ’(t),0) in the domain. The vector above
(r’(t),0,0) in the tangent plane is (r’(t),0,fr[r(t),θ(t)]r’(t))
and the vector above (0,θ’(t),0) in the tangent plane is (0,θ’(t),fθ[r(t),θ(t)]θ’(t)).
The vector lying above (r’(t),θ’(t),0) will then be the sum of
these two vectors, i.e. (r’(t),θ’(t),z’(t)) = (r’(t),0,fr[r(t),θ(t)]r’(t))
+ (0,θ’(t), fθ[r(t),θ(t)]θ’(t))
= (r’(t),θ’(t), fr[r(t),θ(t)]r’(t) + fθ[r(t),θ(t)]θ’(t)).
