Vector Fields 2D
Contents
In three dimensions, a vector field V can be
expressed in
terms of the functions p(x,y,z), q(x,y,z), and r(x,y,z)
as V(x,y,z) = (p(x,y,z),q(x,y,z),r(x,y,z)). 
Note
that for the gradient vector
field, p = fx, q = fy, and r = fz.

Conservative Vector Fields 2D Top of Page
Contents
If a three-dimensional
vector field F(p,q,r) is
conservative, then py = qx, pz = rx,
and qz = ry. 
Since F is conservative, F = ∇f for some
function f and p = fx, q = fy,
and r = fz. By the equality of mixed partials,
py = fxy = fyx =
qx,
pz = fxz = fzx =
rx,
qz = fyz = fzy =
ry. 
[D]
Exercises
1. For each of the following, use the demo to determine
whether or not the vector field F is conservative. If it is
conservative, find the potential function of F.
- F = (x, y, z)
- F = (y - z, x + z, x + 2*y)
- F = ( 1, 1, z)
- F = (cos(x), sin(y), arctan(z))
- F = (x/(x2+y2+z2),
y/(x2+y2+z2), z/(x2+y2+z2))
- F = ( 0, 0, -9.8)
2. In the 2-Variable lab on conservative fields, you have the
option of plotting a surface that represents a function whose gradient
is the vector field. Why will that not work for 3 variables? What could
be used instead?
|
Path Integrals in Three-Space 2D
Top of Page
Contents
If c(t) = (x(t),y(t),z(t)) is a path in three-space and f(x,y,z)
is function defined over c, then the path integral of f
along c is given by ∫c f(x,y,z) ds = ∫abf(x(t),y(t),z(t))s'(t)dt.
where s'(t) = √(x'(t)2 + y'(t)2 + z'(t)2).

If
f(x,y,z) = 1 then the
path integral is simply the arc length of c. 
[D]
Exercises
|
1. While path integrals
can be carried out in two-space and three-space, they could still be
considered to be part of single variable calculus. Why is this?
2. Find the arc length of the curve (cos(t), sin(t),
sin(2t)), 0 ≤ t ≤ 2π.
|
Circulation 2D
Top of Page
Contents
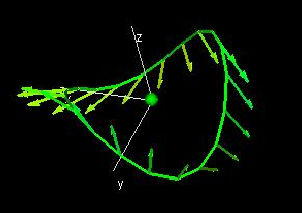
[D]
Curl 2D
Top of Page
Contents
The curl of a
three-dimensional vector field V(x,y,z)
is defined as curl V = ∇ × V = (ry-qz,
pz-rx, qx-py). 
Note
that this is another vector
field. 
If a three-dimensional
vector field F(p,q,r) is conservative,
then its curl is identically zero. 
Using the previous part,
∇ × F = |i
j
k | = (r_y - q_z, p_z -
r_x, q_x -
p_y) = (0,0,0).
|∂/∂
x ∂/∂
y ∂
/∂
z|
|p q
r |


[D]
Flux 2D
Top of Page
Contents

[D]
Divergence 2D Top of Page
Contents
Note
that for the gradient vector
field, p = fx, q = fy, and r = fz.

The divergence of
a three-dimensional vector field V(x,y,z)
is defined as div V = ∇ · V = px + qy
+
rz. 
Note
that divergence is a scalar
value. 
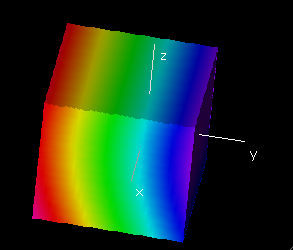
[D]
Exercises
1. In the divergence and curl demos, enter for V the position
function (V(x, y, z) = (x, y, z)). Describe the divergence and
curl of this vector field.
2. Describe the divergence and curl of the vector field V(x,
y, z) = (-y, x, 0).
3. Find the circulation of the vector fields in 1. and 2.
along the unit circle in the xy-plane centered at the origin.
4. Find the flux of the vector fields in 1. and 2. across
each of the following surfaces:
- The sphere of radius 1 centered the origin.
- The sphere of radius 2 centered the origin.
- The cylinder of radius 1 given by x2 + y2
= 1.
- The plane z = 1.
|
Stokes' Theorem for Function Graphs 2D
Top of Page
Contents
Stokes' Theorem states that for some vector field F and
oriented surface S with boundary curve s,
∫∫Scurl F ⋅ dS = ∫s+F
⋅ ds. ("+" indicates
that the direction of travel, projected onto the x-y
plane, is counterclockwise when viewed from above)
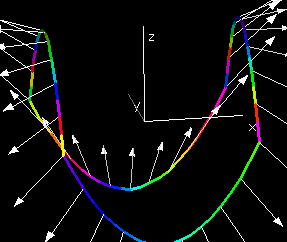
[D]
Surface Integrals over Function Graphs 2D
Top of Page
Contents
The surface integral of a function f(x, y, z) over the
function graph S of a function g(x, y) for some
domain D is defined as follows:
∫∫Sf(x, y, z)dS = ∫∫Df(x, y, g(x, y))√(1 + gx2
+ gy2)dxdy 
Some applications which illustrate the properties of surface
integrals:
When f(x, y, z) = 1, this integral gives the surface area
of S.
If f(x, y, z) is a density function, then the surface
integral gives the total mass of the surface. 

[D]
Exercises
|
1. Find the surface area of the graph of g(x, y) = x2
+ y2, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1.
2. Evaluate
∫∫D(x + y + g(x, y))sqrt(1 + gx2
+ gy2)dxdy
where g(x, y) = xy and D is defined such that 0
≤ x ≤ 1, 0 ≤ y ≤ 1.
|
The surface integral of the vector field F(x, y, z) over
the surface g(x, y) for some domain D is given by
this expression:
∫∫DF(x,y,g(x,y))⋅(-gx(x,y),-gy(x,y),1)dxdy.

[D]
Gauss' Divergence Theorem for Regions between Function
Graphs 2D Top of Page
Contents
According to Gauss' Divergence Theorem,
∫∫∫W(div F)dV = ∫∫∂WF⋅ndS.
for some region W in 3-space and its boundary ∂W.
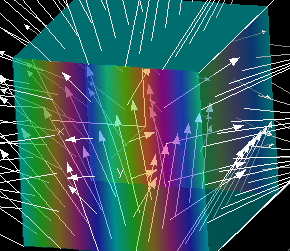
[D]
Exercises
|
Having seen Green's
Theorem applied to divergence in the plane and Gauss' Divergence
Theorem, can you make any conjectures regarding divergence in 4 or more
dimensions?
|