To illustrate the concept of stretching a solid along lines of vision, we decided to use a model of a very simple shape: the cube. This allowed us to get a precise view of just how much one can distort something without losing the visual image. The resulting models where quite interesting, especially as none of had been able to imagine how they would look in the end, especially the more complex view.

The idea was simple: to project the points of a cube along visual lines of perspective and create another cube from these points:

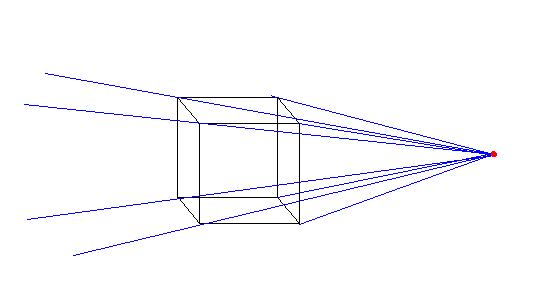
The cubes themselves were constructed from thin wooden dowels and epoxy. We made two different distortions: one from a face, the other from a corner.

The first cube is very simple, viewed from one face, slightly above the plane in which it sits. I ran into problems due to the basic principle of physics which dictates that no two objects can occupy the same space at the same time, because we do not live in the world of mathematically perfect figures and infinitely thin lines. Therefore I decided to simply mark the vertexes along the lines to represent the distorted cube, and build the actual model outside of the strings. In the end, this is much more useful anyway, because it allows one to play with the viewpoint and shadows.

The second cube was constructed in a similar way, but viewed from a different direction and so distorted along different lines. This cube rests on its corner, with the lower of the horizontal corners pointing towards the focal point. The resulting distortion is very puzzling because it does not resemble a cube beyond the fact that it has six faces meeting at eight vertices. It is only symmetrical across one cross-section (vertically and in the direction away from the viewer). It is especially interesting to look at in front of a mirror, as one can "see" the perfect cube close to the eye and yet, in the background, see in the mirror that it is a completely distorted solid.