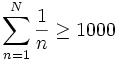| Date |
Sections |
What is covered. Comments |
Homework assignments |
| |
|
|
|
| 1/24 |
s. 1.1 |
Logic, quantifiers. |
Read s.1.1, 1.2, p. 7 #1 a, c, #2 a, c, d, # 3 b |
| 1/26 |
s. 1.2 |
Functions. Comparison of infinite
sets. Countable and uncountable sets |
p. 13 #1, 2, 4, |
| |
|
|
|
| 1/29 |
s. 1.2 |
Properties of countable sets |
|
| 1/31 |
Ch. 2 |
Construction of real numbers: infinite decimal (binary)
fractions and Dedekind cuts.
Read carefully s. 2.1.1 and 2.4.2
Read over the rest of Ch. 2, but do not bother much with
Cauchy sequences, we will return to this topic later.
|
p. 68 # 1, 2 (not collected now)
To be collected Fri. 2/2: p 13 # 4 (find a one line proof), p. 7 # 1 a, 2d |
| 2/2 |
s. 3.1.1 |
Dedekind cuts (continuation).
Completeness of reals. Supremum, infimum. |
p. 84 # 1 (sup, inf only), # 4
Also read the handout about Dedekind cuts |
| |
|
|
|
| 2/5 |
s. 3.1.1- 3.1.2 |
Definition of limit. Main
properties |
Prove that the sequence (-1)-n does not have a limit.
(will be collected Fri,. 2/9)
Read handout #4 about arithmetic operations with limits. |
| 2/7 |
See handout # 4 |
Properties of limits. Completeness
and Cauchy sequences. Limsup and liminf |
Prove Pinching Principle. p. 84 #
2, 5
|
| 2/9 |
|
Cauchy sequences and completeness
(continued) |
|
| |
|
|
|
| 2/12 |
|
Complete metric spaces. Completion.
Equivalence relations, quotient spaces. |
p. 37 # 3, 5, 6, p. 55 # 3 (use
completeness of reals and Cauchy sequences) |
| 2/14 |
See Handout 4 |
Working with limits. |
Click here to
get the assignment (PDF, 36K). This assignment will
be collected Fri. 2/16 |
| 2/16 |
S. 3.2 |
Subsequences, limit points. Open
sets |
Click here to
get the assignment (PDF, 36K). This assignment will be
collected Fri 2/23 |
| |
|
|
|
| 2/19 |
|
President's day. |
|
| 2/21 |
s 3.2 |
Closed sets, accumulation
points. |
p. 98 # 8, 10, 12, 12, 13 |
| 2/23 |
s. 4.1 |
Continuous functions |
Click here to
get the assignment (PDF, 29K). |
| |
|
|
|
| 2/26 |
s. 4.1, 9.2 |
Inverse images of open sets.
Relative topology. |
p 126 # 3, 14, p. 139 # 12, p. 384
# 1 |
| 2/28 |
s. 4.1 |
Limit of a function. Connection
with limit of sequences |
Click here to
get the assignment (PDF, 30K). |
| 3/2 |
s. 4.1 |
Composition of functions. Putting
limit inside the function. |
Click here to
get the assignment (PDF, 33K). |
| |
|
|
|
| 3/5 |
s. 4.2 |
Intermediate value theorem. |
p. 138 # 3 (ignore the question
about open intervals), 4, 7, 8, 17. Will
be collected Fri 3/9 |
| 3/7 |
s. 4.2 |
Compactness |
p. 106 # 1, 6, p 126 # 8, p. 138 #
11, 15 |
| 3/9 |
s. 4.2 |
Compactness, continued. Uniform
continuity. |
Work out examples of continuous but
not uniformly continuous functions. p. 107 # 7, 8 |
| |
|
|
|
| 3/12 |
|
|
|
| 3/14 |
|
Midterm |
|
| 3/16 |
s. 5.1 |
Derivatives. Definitions and main
properties. O and o notation. |
p. 152 # 1-4, 7. Compute
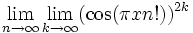
(first take limit as k goes to infinity, and then as n goes to
infinity) |
| |
|
|
|
| 3/19 |
s. 5.1, 5.2 |
Maximum and minimum. Mean value
theorem |
p. 164 # 2, 6, 10, 11, 12 This
assignment will be collected Fri 3.23 |
| 3/21 |
s. 5.2 |
Mean value theorem (continued) |
Read s. 5.3 (calculus of
derivatives).
p. 164 # 3, 13, p. 176 # 1, 2, 3. |
| 3/23 |
s. 5.4 |
Taylor's formula |
p. 176 # 3, 4, 5, 15, p. 192 # 2,
3, 8, 16 |
| |
|
|
|
| 3/26 |
|
Spring recess
|
|
| 3/28 |
|
|
| 3/30 |
|
|
| |
|
|
|
| 4/2 |
s. 5.4 |
Lagrange's remainder theorem |
Click here to
get the assignment (PDF, 41K). This
assignment (except problem #1) will be collected Fri 4/6 |
| 4/4 |
s. 5.4 |
Applications of the Taylor's
formula and Lagrange remainder theorem |
Click here to
get the assignment. This
assignment will be collected Fri 4/6 |
| 4/6 |
s. 5.4 |
|
Prove second mean value theorem,
and get the L'Hopitalle's rule (case 0/0) from it.
p. 194 # 19, 20 |
| |
|
|
|
| 4/9 |
s. 6.1, 6.2 |
Riemann Integral, Definition |
p. 217 # 2, p. 231 # 1, 3, 4, 6
Collected Fri 4/13 |
| 4/11 |
s. 6.1 |
Fundamental theorem of calculus,
properties of integral |
|
| 4/13 |
s. 8.1 |
Logarithm defined as integral |
p. 232 # 9, p 235# 3, p. 335 # 6,
7, p. 218 # 5 |
| |
|
|
|
| 4/16 |
s 7.1, 7.2 |
Series, definitions, convergence,
Cauchy criterion |
p. 262 # 1, 2, 3, 9, 13, 14 This
assignment except # 9 will be collected Fri 4/20 |
| 4/18 |
s. 7.1,7.2 |
Absolutely convergent series,
reordering. Tests of convergence |
Estimate the minimal number N such
that 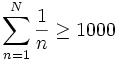 |
| 4/20 |
|
Take home part of the test 2 will
be given |
|
| |
|
|
|
| 4/23 |
|
Test 2 in class part |
p. 274 # 2, 3, 5, 7, 11, 13 a Will be collected Fri
4/27 |
| 4/25 |
s. 7.3 |
Integration and differentiation of
sequences and series. |
|
| 4/27 |
s. 7.4 |
Power Series |
|
| |
|
|
|
| 4/30 |
|
|
|
| 5/2 |
|
|
|
| 5/4 |
|
|
|
| |
|
|
|
| 5/7 |
|
|
|
| 5/9 |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|