In the Orientation page of this document, there is a fairly intuituve explanation as to why time seems to slow down when observers are in relative motion.. The following is a more physical description of what happens to time when the obervers and observees travel at velocities near the speed of light.
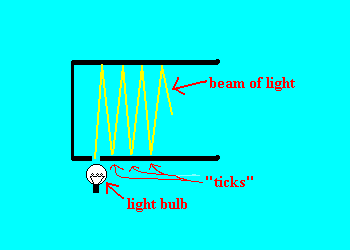
In order to supplement our understanding of the subject, we will use a time keeping mechanism known as a clock--a light clock in this case. A light clock, as shown in Figure 1 consists of a light bulb and two nearly parallel mirrors. A beam of light is sent from the light bulb to the top mirror, then reflected to the bottom, to the top, to the bottom, to the top, etc... Every time the beam of light hits the bottom mirror, we say that a "tick" has happened.

Figure 1: Light Clock
Suppose we take this light clock and accelerate it to to speeds close to the speed of light. Now, instead of going straight up and down, a beam of light travels the path shown in Figure 2. The lights starts at the bulb at t = 1; by the time the light gets to the top mirror (t = 2), the whole clock is shifted over; and by the time the light gets to the bottom mirror (t=3), the wh ole clock is shifted far to the right. So we can see that if the clock is moving fast enough, a tick will only occur when the light has traveled a certain length as well as a certain height.
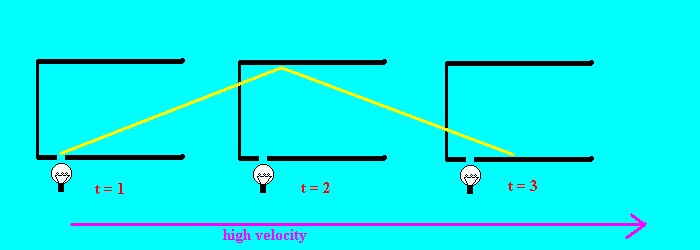
Figure 2: Sushi
Since the speed of light is constant in all frames of reference, and light is travelling a longer distance, the time between ticks is longer. To a person standing on top of the clock, time does not slow down; for in his reference frame, the light is still going straight up and down (at the speed of light). However, to an outside observer, time has slowed down on the light clock.
When bodies undergo acceleration, wacky things happen. With inertial bodies, time slows down mutually (for more, see Orientation). But what if two bodies meet at point A, accelerate at different speeds, and then meet at the same event (point B). If time slowed down mutually, could they ever be at the same event again? The answer is 'no'. In fact, if two bodies meet at point A, accelerate to different speeds, and then meet at point B, they will notice that a different amount of time has elapsed for the two of them. This is usually phrased in term of the twin paradox: If one of two twins goes on a a wildly acclerating, near speed-of-light escapade while the other twin stays at home and plays bridge, they will find that (if they meet again) they have different chronological ages.
Figure 3: Minkowski Diagram of the Twin Paradox
Spockrates gives a much clearer explanation of the twin paradox
than this author can. Read ON PROCESSED MEAT AND
SPACETIME