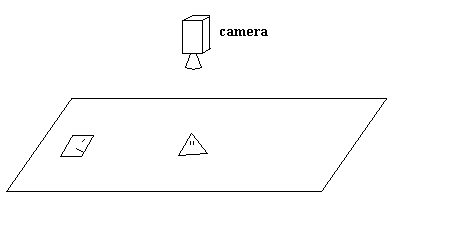
The constancy and finiteness of the speed of light provides some very interesting questions regarding simultaneity. For example, consider the diagram below:

Figure 1: Flatland Photoshoot
The camera lies above Flatland and is taking a series of photographs (like a video camera). In order to get a spacetime representation of the scene, one could stack the individual photographs. If stacked on a tabletop with the pictures facing up, time is also in the 'up' direction.
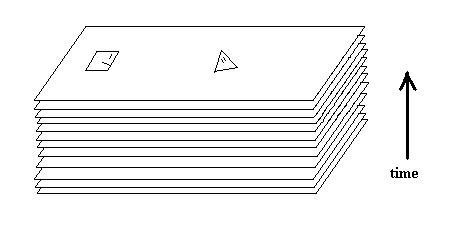
Figure 2: Photograph Spacetime
The key idea here is that, since the square is farther from the camera than the triangle, it takes longer for light to get from the square to the camera than from the triangle to the camera. What this means is that the light entering the camera contains photons that left the triangle a time t ago, and photons that left the square a time t' ago. Since the square is farther than the triangle, t' is greater than t. In other words, when the camera takes a snapshot of the scene, the camera's image of the square is an older image than the camera's image of the triangle. Pictures do not show the square and triangle at the same time!
There are two ways to get slices of simultaneity from the stack of photogrpahs shown above. It has already been shown that each photograph contains an image of the triangle and an older image of the square. Therefore, in order to get a slice of simultaneity, one could take a curved slice of the photographs like so:
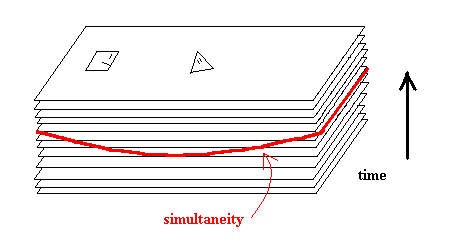
Figure 3: A Simultaneous Slice of Spacetime
...or one could bend the photographs and take horizontal slices like so:
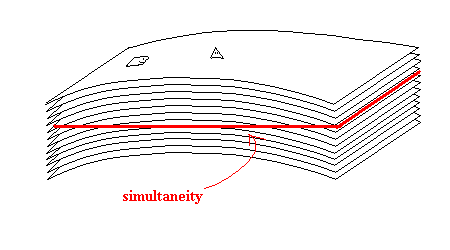
Figure 4: The Fourth Figure
The above is a good description of what happens with a stationary camera. But what if the camera is moving? It will be shown below that a a slice of simultaneity for a moving camera would be a diagonal slice (in Figure 4). In fact, it is possible to calculate the angle of this slice. These calculations will be made with the trusty Minkowski Diagrams which are much more easy to manipulate than stacks of photographs.
When observers are in relative motion, they have simultaneities that are at odds with one another. Before this issue is explored, however, one should understand the relativity of time. The following is a Minkowski Diagram of two observers in relative (inertial) motion (using observer A as a reference frame).
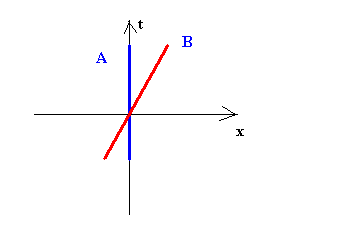
Figure 5: Two Non-accelerating Observers
Now suppose that observer A sends out a light signal to B at intervals of one second.
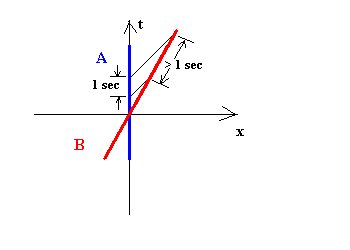
Figure 6: A Signalling B
On A's world line, the signals occur exactly one second apart. However, on B's world line, the signals occur at intervals greater than one second. Relative to A, B's time has slowed down! If A were to look out his window at B, he would see B's time running slowly.
An important point here is that if B were to look out of his window, he would see A's time slow down in exactly the same manner. An easy way to see this is to look at the same Minkowski diagram with B as the reference frame. It is simply the mirror of Figure 6.
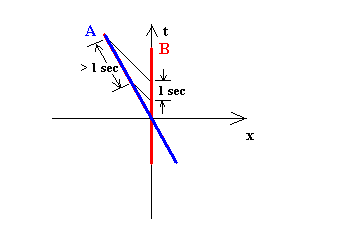
Figure 7: B Signalling A
Measuring the intervals between signal transmission and reception is an efficient method for calculating the line (or plane) of simulataneity for observers in inertial motion. Consider the Figure 8:
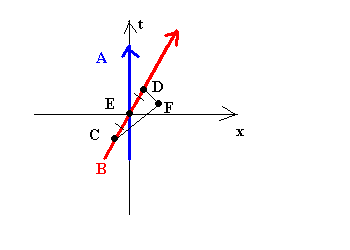
Figure 8: Measuring Simultaneity
In Figure 8, B (while at C) sends a light signal to F. A and B cross paths at E. F receives B's the signal and reflects it back to B; and B receives the signal back at D.
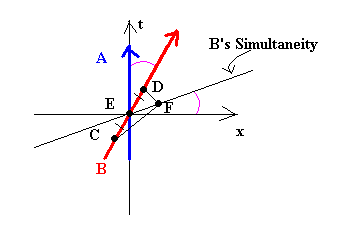
Figure 9: B's Simultaneity
Because the line segments CE and ED are of equal length on B's world line, E is a midpoint of CD for B. Because the reflection of the signal happens at F, B can only assume that F is also a midpoint of CD. Therefore, B's line of simultaneity is always parallel to the line passing through E and F (he thinks they happen at the same time). (A's simultaneity is horizontal.) In general, the angle B's motion makes with the time axis is equal to the angle B's line of simulataneity makes with the position axis. Therefore, if B were to move at the speed of light (a 45 degree angle), time would stand still; and if B were to find a way to travel infinitely fast, his slice of simultaneity would be vertical--one slice of space through all of time. Maybe this is how the great astronomers of Einstein At The Bat got together...
For more zany fun with Spacetime orientation, read about Haikube.