|
Critical Points
(Page: 1 | 2
) Text A critical point of a function of one variable, f(x), is a value of x such that the tangent line is horizontal.
 If f(x) is a differentiable function, then x0 is a critical point if and only if f'(x0) = 0.
If f(x) is a differentiable function, then x0 is a critical point if and only if f'(x0) = 0.

Demos
Critical Points

| 
|
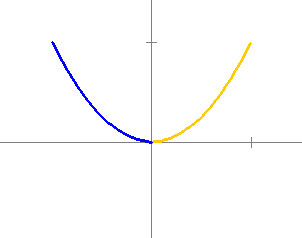
In this demonstration, the function f(x) and its domain are defined in the control panel. The graph of the function is colored blue where it is decreasing and orange where it is increasing. 
|
Exercises 1. Try typing in the function f(x) = x2 - x4. Characterize the points on the graph where the color changes from blue to yellow and from yellow to blue.
2. Can we use this color coding to identify inflection points?
|