|
Critical Points
(Page: 1 | 2
) Text A critical point of a function of two variables f(x,y) is a point such that the tangent plane is horizontal.
If f(x,y) is a differentiable function, then (x0,y0) is a critical point of f(x,y) if and only if fx(x0,y0) = 0 and fy(x0,y0) = 0.
Demos
Critical Points
| 
|
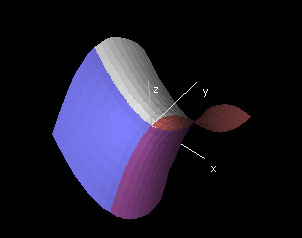
In this demonstration, the "Function Graph: f(x,y)" window shows the graph of f color coded by the sign of the partials derivatives.
Purple represents fx > 0 and fy > 0.
Red represents fx > 0 but fy < 0.
Blue represents fy > 0 but fx < 0.
White repsesents fx < 0 and fy < 0.
In the second window, "fx(x,y) > 0", just that part of the surface where the x-derivative is greater than zero is colored (in red). The window "fy(x,y) > 0" allows you to view just the region of the surface where fy is greater than zero (in blue). The rotations of these two windows are linked with the main window, so even rotating the surface around you will see how the colored regions from the main window are obtained by just "adding up" the colorations of the minor windows. I.e. the coloring is purple if and only if both fx(x,y) and fy(x,y) are greater than zero.
|
Exercises 1. Note the clockwise order of the colors around the saddle points in the graph; red, purple, blue, white. Now enter f(x,y) = x2 + y2. Is the sequence red, purple, blue, white in clockwise or counter-clockwise order around the minimum in this graph? What about for the maximum in f(x,y) = -x2 - y2?
2. What does the orientation of the colors tell you about the type of critical point?
3. Try entering f(x,y) = -x4 + x2 - y2, which has three critical points visible. Based on your answer to the last exercise, what type of critical points are each of these three?
4. Why do critical points only occur at corners which border all four colors?
5. Analyze the function f(x,y) = (y-x2)(y-1). What can we say about the 0 level sets of f(x,y), fx(x,y), and fy(x,y)?
6. Analyze Crater Lake shifted by an earthquake, with function f(x,y) = -(x2 + y2)2 + 2(x2 + y2) + mx for various values of m. For which m will the lake no longer hold water? Describe the critical levels, i.e. the level sets that contain critical points.
|