|
Critical Points
Text A critical point of a function f(x, y, z) is a point such that the tangent plane is horizontal.
 If f(x, y, z) is a differentiable function, then (x0,y0,z0) is a critical point of f(x, y, z) if and only if fx(x0,y0,z0) = fy(x0,y0,z0) = fz(x0,y0,z0) = 0.
If f(x, y, z) is a differentiable function, then (x0,y0,z0) is a critical point of f(x, y, z) if and only if fx(x0,y0,z0) = fy(x0,y0,z0) = fz(x0,y0,z0) = 0.

Demos
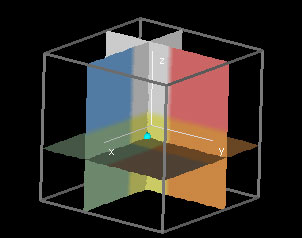
Critical Points

| 
|
This provides a geometrical interpretation of critical points of a function of three variables. You can use the hotspot in the - window to move around the turquoise point in the 4D Color Graph and the slices. The color graph is colored according to the value of the , and -partials at that point. If the x-partial is positive, then the point is colored red; if the y-partial is also positive, then a blue layer is added, and if the z-partial is also positive, then a yellow layer is added. At a point where a partial is zero, we can observe a transition of color.
A critical point is a point where all three partials are zero, so it's a point where we observe a change of color in every direction. Hence, it must be a point where all eight colors meet. 
|
Exercises 1. Consider each of the three slice surfaces separately. How does the clockwise order of the coloring relate to the type of critical point found on that slice surface where the four colors meet?
2. If the critical point on the graph of f(x, y, z) is a maximum, what can you say about the critical points on each of the slice surfaces?
3. If the critical point on the graph of f(x, y, z) is a saddle, what can you say about the critical points on each of the slice surfaces?
4. If the critical point on the graph of f(x, y, z) is a minimum, what can you say about the critical points on each of the slice surfaces?
5. In the demo, enter the function f(x, y, z) = x4 - 5x2yz + y2 + z2 and set the hotspot at the point (0, 0, 0). The critical points on all three slices are local minima. Does this mean that the point (0, 0, 0) is a local minimum of the function f(x, y, z)? Why or why not?
|