Domains, Ranges, & Function Graphs of Parametric Equations
1D
3D
Rectangular Coordinates
Contents
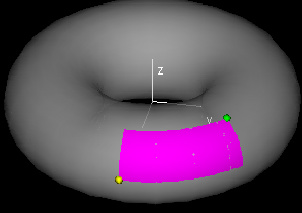
A parametric surface in three space
(x(u,v),y(u,v),z(u,v)) is
given by three coordinate functions x(u,v), y(u,v) and z(u,v) of the variables (u,v) defined over the same
domain in the (u,v)-plane.
This common domain is called the domain
of the parametric surface. 
The
range of a parametric surface
is the collection of all points in three-space
(x(u,v),y(u,v),z(u,v))
for all
(u,v) in the
domain of the surface.

[D]
Exercises
Describe the parametric surface (cos(u)cos(v),sin(u)cos(v),sin(v))
where -π ≤ u ≤ π and -π/2 ≤
v ≤ π/2 . What are the ranges
of the three coordinate functions x(u,v)
= cos(u)cos(v), y(u,v) = sin(u)cos(v) and z(u,v) = sin(v)?
Same question for (v
cos(u), v sin(u), v).
Same question for ((2+cos(v))cos(u),
((2+cos(v))sin(u),sin(v)).
What is the relationship between the range of (x(u,v),y(u,v),z(u,v)) and the
ranges of x(u,v), y(u,v) and z(u,v)?
|
Slice Curves in Parametric Equations Polar Coordinates
Rectangular
Coordinates Top of Page
Contents
We can describe a slice curve with x = x0 as a
parametric curve x(t) = x0, y(t) = t, so f(x(t),y(t))
= f(x0,t). 
Similarly
the slice curve with y
= y0 can be given as (x(t),y(t),f(x(t),y(t))) =
(t, y0,f(t,y0)). 
The slice curve through (x0,y0) with
slope m can be
described as (x0 + t. y0 + mt, f((x0
+ t. y0 + mt). 
In
polar coordinates, this can be
written (x0 + tcos(θ0), y0 +
tsin(θ0),f(x0 + tcos(θ0), y0
+
tsin(θ0)), where m = tan(θ0). 
In general the slice curve over the parametric curve (x(t),y(t))
in the domain of a function f is the curve (x(t),y(t),f(x(t),y(t))).
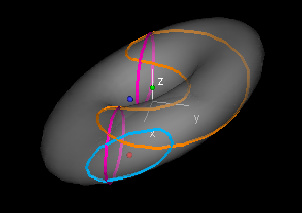
Slices of Parametric Surfaces
For every point (u0,v0) in the domain of a
parametric function f, the u0-parametric curve is X(u0,v)
= (x(u0,v),y(u0,v),z(u0,v)). The
domain of the u0-slice curve is the set of y for which (u0,v)
is in the domain of f.
Similarly we define the v0-parametric curve to be X(u,v0)
for all u such that (u,v0) is in the domain of f.
Level Sets & Contours in Parametric Equations
1D
Polar
Coordinates
Rectangular Coordinates
Top of Page
Contents
Given a parametric surface in three-space, we can consider the contours
for any of the three coordinate functions.
For example, the level set x = k for the surface (x(u,v),y(u,v),z(u,v))
is the set of points (u,v)
in the domain such that x(u,v) =
k. The x-contour at height k is the
collection of all points (x(u,v),y(u,v),z(u,v))
where x(u,v) = k.
Geometrically the x-contour
of the surface is the intersection of the graph of the surface and the
plane x = k in
three-space. The analogous definitions give the y-level sets and y-contours, and the z-level sets and z-contours.
[D]
Exercises
Describe the x-,
,y-, and z-contours for the surface (cos(u)cos(v),sin(u)cos(v),sin(v))
where -π ≤ u ≤ π and -π/2 ≤
v ≤ π/2.
Same question for the surface (v cos(u), v sin(u), v), where -π
≤ u ≤ π and where v is any
real number.
Find the x = 0
level set and the x = 0
contour for the surface ((2+cos(v))cos(u),
((2+cos(v))sin(u),sin(v)) where -π ≤ u ≤
π and -π/2 ≤ v ≤ π/2.
What about the level sets and contours for y = 0 and for z = 0?
|
Continuity in Parametric Functions 1D 3D Polar Coordinates
Rectangular Coordinates
Top of Page
Contents
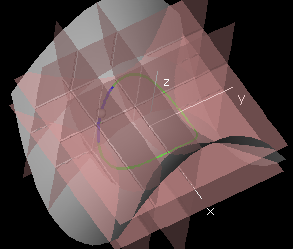
If x(u,v), y(u,v), and z(u,v) are continuous functions of u and v, and
if u(t) and v(t) are continuous functions of t near t=t0, then the
parameterized curve (x(u(t),v(t)), y(u(t),v(t)), z(u(t),v(t))) in
3-space is a continuous funciton of t.
[D]




