Domain and Range in Polar Coordinates Rectangular
Coordinates Cylindrical
Coordinates Contents
Slice Curves in Polar Coordinates Parametric Equations
Rectangular Coordinates
Cylindrical
Coordinates Top of Page Contents
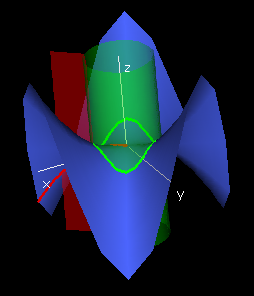
For every point (x0,y0) in the domain of
a function f, the intersection of the graph of f with the vertical
plane above the line (x0 + rcos(θ0), y0
+ r sin(θ0)) will be the θ0-slice curve
((x0 + rcos(θ0), y0 + r sin(θ0),
f[r,θ0]). The domain of the θ0-slice
curve is the set of r for which (x0 + rcos(θ0),y0
+ rsin(θ0)) is in the domain of f.
Similarly we define the r0-slice curve to be the portion of
the circle (x0 + r0cos(θ),y0, + r0sin(θ),
f[r0,θ]) for all θ such that (x0 + r0cos(θ),
y0, + r0sin(θ)] is in the domain of f.
Level Sets and Contours in Polar Coordinates Parametric Equations
Rectangular Coordinates
Cylindrical
Coordinates
Top of Page Contents
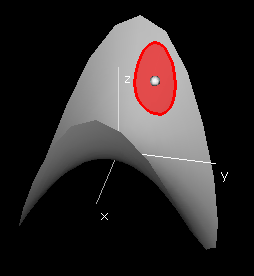
The collection of all points [r,θ] in the domain of a polar
coordinate
function f for which f[r,θ] = k is called the level
set of f at level k. 
The level set of f is
empty if there is no point [r,θ] in the domain of f
for which f[r,θ] = k. For most functions we will encounter,
for almost all constants k, the level set will consist of one or more
curves in the domain, possibly intersecting, as well as single points. 
The collection of points (r*cos(θ), r*sin(θ), f[r,θ]) in the graph of the function
f such that f[r,θ] = k is called the contour of f at height k.
Exercises
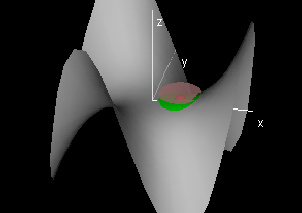
Analyze Crater Lake shifted by an earthquake, with function
f[r,θ]= -r4 + 2r2
+ mrcos(θ) for various values of m. For which m will the lake no longer
hold water? Describe the critical levels, i.e. the level sets that
contain critical points.
|
Continuity in Polar Coordinates Parametric Equations
Rectangular Coordinates
Top of Page Contents
According to the epsilon-delta definition, a function f of
two real variables is said to be continuous at (x0,y0)
if for any ε > 0 there exists a δ such that |
f(x,y) - f(x0,y0) | < ε whenever the
distance between (x,y) and (x0,y0)
is less than δ.
When we are operating in polar coordinates, we may consider x =
x0 + r cos(θ), y = y0 + r sin(θ), in which
case the distance between (x,y) and (x0,y0)
is | r |. Given any ε > 0, we then have to show
that there is
a δ such that | f(x,y) - f(x0,y0)
| < ε whenever | r | < δ.
[D]