|
Directional Derivative
Text The directional derivative for a function f(x,y) in the direction θ is denoted ∇θf(x,y) and is the derivative of the height function z(t) in that direction.

Consider a point P = (x0,y0) in the domain of f(x,y). The line in the domain corresponding to the direction θ will have the parametric form (x0 + t cos θ, y0 + t sin θ) and the height function z(t) associated with the slice curve along this line will have the form z(t) = f(x0 + t cos θ, y0 + t sin θ).

The directional derivative ∇θf(x0,y0) at the point P will be the derivative evaluated at t = 0 of the height fuction z(t)
∇θf(x0,y0) = z'(t) |t=0 = ∂/∂t (f(x0+t*cos(θ),y0+t*sin(θ)))|t=0.

Note that the partial derivatives fx and fy are just the directional derivatives at θ = 0 and θ = π/2, respectively.
Also note that the directional derivative is a function of the direction variable θ; the variable t is only used as a parameter.

Demos
Tangent Line to Slice Curves

| 
|
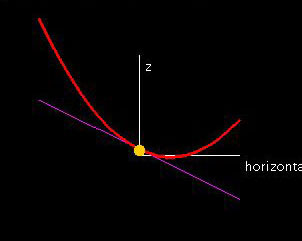
Recall from Lab 2 that the partial derivatives of a function f(x,y) at a point (x0,y0) can be found by looking the x- and y-slice curves of the function graph and then calculating the slopes of the tangent lines to these curves at (x0,y0,f(x0,y0). For the directional derivative, instead of slicing along the positive x- and y-directions, we slice the graph along a direction (cos θ, sin θ). The slope of the tangent line to the slice curve at (x0,y0, f(x0,y0) is the directional derivative. The demo allows you to choose a point (x0,y0) in the domain as well as a direction (cos θ, sin θ) using the two orange hotspots. The graph is shown in a separate window with the corresponding slice curve and slicing plane. The third window shows the slice curve in its plane along with the tangent line. 
|
Exercises Find the value of θ for the maximum directional derivative of any slice curve. What θ gives the minimum directional derivative for this same slice curve? How are these values related? Try this for several different slice curves.
|