|
Taylor Series
Text Taylor series are polynomials that approximate functions.
For functions of two variables, Taylor series depend on first, second, etc. partial derivatives at some point (x0, y0).

Let P1(x,y) represent the first-order Taylor approximation for a function of two variables f(x,y). The equation for the first-order approximation is P1(x,y) = f(x0,y0) + (x - x0)fx(x0,y0) + (y - y0)fy(x0,y0). We are already quite familiar with this equation as it defines a tangent plane.
Let P2(x, y) represent the second-order Taylor approximation. Its equation is P2(x,y) = f(x0,y0) + (x - x0)fx(x0,y0) + (y - y0)fy(x0,y0) + 1/2(x - x0)2fxx(x0,y0) + (x - x0)(y - y0)fxy(x0,y0) + 1/2(y - y0)2fyy(x0,y0). To simplify, we can subsitute g(x,y) (the first order Taylor approximation) for the first three terms: P2(x,y) = P1(x,y) + 1/2(x - x0)2fxx(x0,y0) + (x - x0)(y - y0)fxy(x0,y0) + 1/2(y - y0)2fyy(x0,y0)
In general, the nth order taylor approximation for a function f(x, y) is the polynomial that has the same nth and lower partial derivatives as the function f(x, y) at the point (x0, y0).

Demos
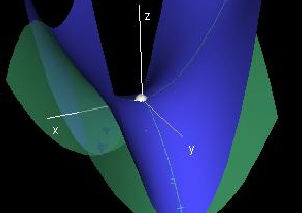
The Tangent Paraboloid

| 
|
This is a demo that shows the tangent paraboloid to a point on a surface (x,y,f(x,y)), as an illustration of the second order taylor approximation in two dimensions. We expand f(x,y) as a Taylor series around the hotspot C, and drop all terms of order 3 or higher. To see that this is but an approximation of the surface, we look at surfaces that are the function graph of a function f(x,y) with degree {geq} 3. Note that for deg f = 2 or less, the second order taylor approximation is exact.

|
Exercises 1. Try entering for f(x,y) several polynomial functions of degree less than 3. What do you notice?
2. Now enter for f(x,y) any polynomial function whose x terms have degree less than 3 but whose y terms may have degrees of 3 or greater. (For terms involving both x and y, the exponent of x should never exceed 2. e.g.: x2y3 is an acceptable term.) For example, try the function f(x,y) = y4 + xy2 + x2 + x + y. Compare the results to those of exercise 1.
3. Enter the expression 1/(x + 1) + 1/(y + 1) for f(x,y). Notice that the tangent paraboloid is not the same as the function graph. Why canít we apply the degree less than 3 rule here?
|