|
Partial Derivatives
Text The partial derivatives of a function of two variables are the slopes of the slice curves.
 If f(x,y) is a function of two variables, then for each y = y0, the function f(x,y0) is a differentiable function of x, and its derivative is denoted fx(x0,y0), called the first partial derivative of f with respect to x.
If f(x,y) is a function of two variables, then for each y = y0, the function f(x,y0) is a differentiable function of x, and its derivative is denoted fx(x0,y0), called the first partial derivative of f with respect to x.
Similarly the derivative of the x = x0 slice curve f(x0,y) with respect to y is denoted by fx(x0,y0), called the first partial derivative of f with respect to y.

Demos
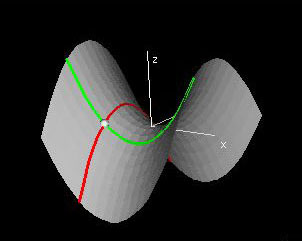
Tangent Lines to Slice Curves

| 
|
The demonstration builds upon the idea of x- and y-slice curves that was introduced in the previous lab. Choose a point (x0, y0) using the white hotspot in the domain window. The graph window shows the point (x0,y0,f(x0,y0) on the surface and the x- and y-slice curves passing through it. The other two windows show the tangent lines to the x- and y-slice curves at (x0,y0,f(x0,y0)). The slopes of these tangent lines are the partial derivatives fx and fy evaluated at (x0,y0). 
|
Exercises 1. Position the hotspot at the origin. What are the slopes of the tangent lines at this point?
2. Where are the slopes of the tangent lines the greatest for both slice curves?
3. Investigate the slopes of the tangent lines at several points on the graph. How are the slopes related to the steepness of the function graph in the x- and y-directions?
4. Move the hot spot to the first quadrant of the domain, then the second quandrant, third quadrant, and fourth quadrant. What can you say about the sign of the slopes of the tangent lines in each quadrant?
5. Investigate the tangent lines for other functions, such as f(x,y) = x2 + y2 or f(x,y) = x2 - 2xy - y2.
|