|
Directional Derivative
Text The directional derivative ∇θφf(x0,y0,z0) at the point P will be the derivative evaluated at t = 0 of the height fuction z(t)
nablaθφf(x0,y0,z0) = z'(t)|t=0 = ∂/∂t (f(x0+t*cos(θ)cos(φ),y0+t*sin(θ)cos(φ), z0+t*sin(φ)))|t=0.
Demos
Tangent Line to Slice Curves

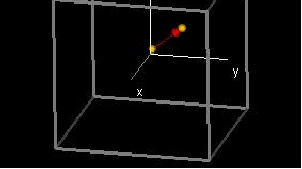
| 
|
In this demo, you can choose a point in the three-dimensional domain using a hotspot. Moving around the second hotspot, which has a vector associated to it, you can choose a direction. The Color Graph window shows the standard color graph, together with the line (drawn in white) that goes through the chosen point P and in the direction of the chosen vector.
The Slice Curve window then graphs the value of the function f(x,y,z) on the chosen line. The color at each point of this graph corresponds to the function value at that point, and to the color in the Color Graph. At the point P, we show the tangent line.The slope of the tangent line is the directional derivative at P in the direction of the orange vector chosen in the demo. 
|
Exercises 1. Evaluate the directional derivatives for each of the sets of conditions below:
- f(x, y, z) = x + y + z, (x0, y0, z0) = (1, 0, -1), θ = 0, φ = 0
- f(x, y, z) = x2 + y2 + z2, (x0, y0, z0) = (0, 0, 0), θ = π/4, φ = π/4
- f(x, y, z) = x2 + sin(y) + ez, (x0, y0, z0) = (5, π/4, 1), θ = π/2, φ = 5π/6
2. What restrictions must be set on the function f(x, y, z) in order for the directional derivative at the origin to be the same in all directions (hint: one of them is f(x, y, z) = f(-x, y, z))?
|