|
Taylor Series
Text Taylor series are polynomials that approximate functions.
For functions of three variables, Taylor series depend on first, second, etc. partial derivatives at some point (x0, y0, z0).

The tangent hyperparaboloid at a point P = (x0,y0,z0) is the second order approximation to the hypersurface.
We expand the hypersurface in a Taylor series around the point P
| f(x,y,z) = |
f(x0,y0,z0) + (x - x0)fx(x0,y0,z0) + (y - y0)fy(x0,y0,z0) + (z - z0)fz(x0,y0,z0)
+ 1/2( (x - x0)2fxx(x0,y0,z0) + (x - x0)(y - y0)fxy(x0,y0,z0) + (x - x0)(z - z0)fxz(x0,y0,z0)
+ (x - x0)(y - y0)fyx(x0,y0,z0) + (y - y0)2 fyy(x0,y0,z0) + (y - y0)(z - z0)fyz(x0,y0,z0)
+ (z - z0)(x - x0)fzx(x0,y0,z0) + (z - z0(y - y0)fzy(x0,y0,z0)
+ (z - z0)2fzz(x0,y0,z0) ) + R3(x,y,z) |
and then we drop the terms of order 3 or higher to get the tangent hyperparaboloid PB(x,y,z)
| PB(x,y,z) = |
f(x0,y0,z0) + (x - x0)fx(x0,y0,z0) + (y - y0)fy(x0,y0,z0) + (z - z0)fz(x0,y0,z0)
+ 1/2 ( (x - x0)2fxx(x0,y0,z0) + (x - x0)(y - y0)fxy(x0,y0,z0) + (x - x0)(z - z0)fxz(x0,y0,z0)
+ (x - x0)(y - y0)fyx(x0,y0,z0) + (y - y0)2fyy(x0,y0,z0) + (y - y0)(z - z0)fyz(x0,y0,z0)
+ (z - z0)(x - x0)fzx(x0,y0,z0) + (z - z0(y - y0)fzy(x0,y0,z0) + (z - z0)2fzz(x0,y0,z0) ) |
In general, the nth order taylor approximation for a function f(x, y, z) is the polynomial that has the same nth and lower partial derivatives as the function f(x, y, z) at the point (x0, y0, z0).

Demos
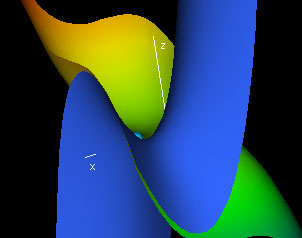
Slicing the Tangent Hyperparaboloid

| 
|
Observe that the tangent hyperparaboloid PB depends on the same number of variables as the function f, i.e. on 3 variables. Therefore, the tangent hyperparaboloid to a function of three variables cannot be visualized directly; it lies in 4-space.
However, we can slice the tangent hyperparaboloid along the x-, y- and z-axes. If each point (x,y,z,f(x,y,z)) has a tangent hyperparaboloid then slicing the surface together with the tangent hyperparaboloid at a given point yields three paraboids that are tangent to the respective slice surface of the hypersurface.
In this demo, you can view these x-, y- and z-slices of the tangent hyperparaboloid. 
|
Exercises 1. Try entering for f(x, y, z) various polynomial functions of degree ≤ 2. What do you notice? Why should this result be expected?
2. Enter for f(x, y, z) the expresssion x2 + y2 + z3. Describe the accuracy of each of the three slices of the Taylor approximation.
3. How does the Hessian matrix of the tangent hyperparaboloid at some point (x0, y0, z0) of the function f(x, y, z) relate to the Hessian matrix of the function itself at that point?
|