|
Moment of Inertia
Text The moment of inertia I of an object about an axis of rotation is a value which indicates the resistance of that object to changes in rotation about that axis. For a region D in the plane with area density ρ(x, y), this calculated using the following formula:
I = ∫(r(x, y))2ρ(x, y)dxdy
Where r(x, y) is the distance of the point (x, y) from the axis of rotation. In the two-dimensional case, this axis is a point.

For an object of density 1, the moment of inertia will be the density multiplied by the integral
I = ∫(r(x, y))2dxdy.

Demos
Moment of Inertia

| 
|
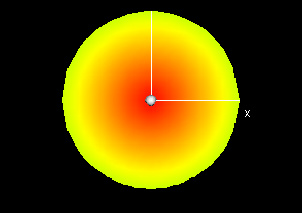
This demo finds the moment of inertia for a region in the plane of uniform density. The bounds of y are expressed as functions f and g of x.
The graph shown displays the region, coloring each point based on its distance from the center of rotation. The closer a point mass is to the center of rotation, the less it adds to the moment of inertia. 
|
Exercises 1. Find the moment of inertia of a circle of radius 1 and uniform density 1, rotated about its center.
2. Find the moment of inertia of a circle of radius R, uniform density, and total mass M, rotated about its center.
3. Find the moment of inertia of a circle of radius R, uniform density, and total mass M, rotated about a point P which is displaced by (x0, y0) from the center of the circle.
4. What formula can you suggest which relates the moment of inertia of an object rotated about a point A to the moment of inertia of the same object rotated about a different point B?
|