|
Surface Area for Function Graphs
Text If a function is differentiable, then one can approximate the graph of the function close to any point as the tangent plane to the graph at that point.
 Recall that the tangent plane to a graph of f(x,y) at some point (x0,y0,z0) is given by z - z0 = fx(x0,y0)*(x - x0) + fy(x0,y0)*(y - y0).
Recall that the tangent plane to a graph of f(x,y) at some point (x0,y0,z0) is given by z - z0 = fx(x0,y0)*(x - x0) + fy(x0,y0)*(y - y0).

We can approximate the area of a function graph by finding the area of a set of parallelogram-shaped fragments of tangent planes, which we will refer to as "shingles", all of which project onto rectangles of area dx * dy in the x-y-plane.

The first step in finding the area of a shingle is to find the vectors which describe the sides of this shingle, one must consider what happens as one moves along a tangent plane to a point some distance either in the x or y direction from the point.
If one moves a distance dx in the x direction, the resulting vertical displacement will be fx(x0,y0)*dx. The vector for the resulting side of the shingle, then, is (dx, 0, fx(x0,y0)*dx). Likewise, movement a distance dy in the y direction will generate the vector (0, dy, fy(x0,y0)*dy).
In general, we can find the area of a parallelogram by taking the magnitude of the cross product of the vectors which describe its sides.
The cross product of (dx, 0, fx(x0,y0)*dx) and (0, dy, fy(x0,y0)*dy) is (fx(x0,y0)dxdy, -fy(x0,y0)dydx, dxdy), so the magnitude is √((fx(x0,y0)dxdy)2+ (-fy(x0,y0)dydx)2+ (dxdy)2) =√(fx(x0,y0)2+fy(x0,y0)2 +1)dA.
The last step is to integrate the area of shingles over some domain D to get the formula for the surface area of a graph:

A(S) = ∫∫D√(fx(x0,y0)2+fy(x0,y0)2 +1)dA
Demos
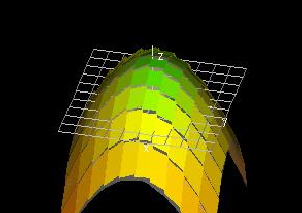
Shingle Approximation of Area

| 
|
This demo shows how the shingle approximation works for the graph of a function f(x, y). Increase the resolution to get a better approximation. Try changing f(x, y) as well. 
|
Exercises In the default example (paraboloid), which approximation is greater: the area of 1 shingle (resolution 1), or the total of the areas of 100 shingles (resolution 10)? You do not need to calculate.
|