Differentiation

Derivatives 2D 3D Parametric Equations Contents

A function f is “differentiable at a point x₀” if there is a well-defined tangent line at the point (x₀,f(x₀)), i.e. if there is a line L(x) = p(x-x₀) + f(x₀) which is closer to the graph than any other line through the point. If such a line exists, then the slope p is called the “derivative of f at x₀”, denoted “f’(x₀)”.

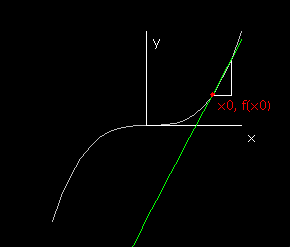
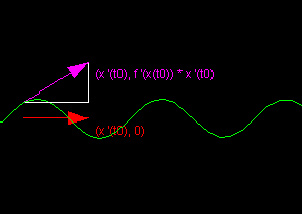
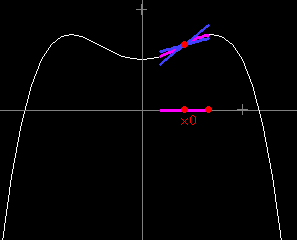
For any non-zero number h, the line through (x₀,f(x₀)) and (x₀+h,f(x₀+h)) will have slope (1/h)(f(x₀+h)-f(x₀)) and the condition for the existence of this tangent line is that the limit as h goes to zero of (1/h)(f(x₀+h)-f(x₀)) = f’(x₀), a well-defined real number.

In terms of an epsilon-delta definition, we say that f is differentiable at x₀ if there is a number f’(x₀) so that fore every ε > 0 it is possible to find a δ such that
|(1/(x-x₀))[f(x) – f’(x₀)(x-x₀) – f(x₀)]| < ε if |x-x₀| < δ.

If f’(x₀) exists for every x₀ in the domain of f, then f is said to be a “differentiable function”. Then f’(x) is a new function derived from f(x), called the “derivative of f at x”.

[D]

Exercises

1. Show that if f(x) = 0 for all x, then f’(x) = 0, and if f(x) = k, a constant, then f’(x) = 0 for all x.

2. Show that if f(x) = px + k, then f’(x) = p for all x.

3. Show that f(x) = |x| is not differentiable at 0, but it is differentiable at all x₀ not equal to zero.

4. Show that the function f(x) = sin(1/x) if x ≠ 0 and f(0) = 0 is not differentiable at 0. Same question for g(x) = xf(x). Show however that h(x) = x²f(x) is differentiable at 0.

5. Prove the basic rules for differentiation: (f+g)’ = f’ + g’, (cf)’ = cf’ for any constant c, (fg)’ = f’g + fg’, (f/g)’ = (gf’-fg’)/g² at any point where 1/g is defined, and (xⁿ)’ = nx^(n-1) for any positive integer n.

Critical Points 2D 3D Parametric Equations Top of Page Contents

A “critical point” of a function of one variable, f(x), is a point x such that f’(x) = 0. At such a point, the tangent line will be horizontal. At a point x where f’(x) > 0, the function f is said to be “increasing” and where f’(x) < 0, it is said to be “decreasing”.

[D]

Exercises

Find the critical points of the following functions and indicate where they are increasing and where they are decreasing.
1) f(x) = k
2) f(x) = px + k
3) f(x) = ax² + 2bx + c
4) f(x) = x³ + ux
5) f(x) = x⁴ +ux²

Tangent and Normal Lines 2D 3D Parametric Equations Top of Page Contents

Recall that if a function f(x) is differentiable at x₀, then the “tangent line to the graph of f at (x₀,f(x₀))” is given by the equation T(x) = f(x₀) + f '(x₀)(x - x₀).

The “normal line to the graph of f at (x₀,f(x₀))” is the line through the point perpendicular to the tangent line. At a critical point, the normal line is the vertical line x = x₀, and at a non-critical point, the slope of the normal line is the negative reciprocal of the slope of the tangent line so the normal line is N(x) = f(x₀) + (-1/f’(x₀))(x-x₀).

[D]

Exercises

1. Find equations for the tangent line and the normal line for each of the following sets of conditions, and check using one of the demos:

f(x) = x² at x = 1
f(x) = sin(x) at x = π
f(x) = |x| at x = 1

2. Find the x- and y- intercepts of the tangent line to f(x) = 1/x at the point x = 1. Find the area of the triangle with vertices the origin and the x- and y-intercepts. Same question for the point x = x₀ for a given positive number x₀.

Chain Rule 2D 3D Top of Page Contents

The chain rule expresses the derivative of the composition of two functions in terms of the derivatives of the functions. Specifically, if x(t) is a differentiable function of t and f(x) is a differentiable function of x, then y(t) = f(x(t)) is a differentiable function of t and y'(t) = f'(x(t)) x'(t).

We can interpret the chain rule for a parametric curve (x(t),y(t)) geometrically. If the curve lies on the function graph y = f(x), then y(t) = f(x(t)). We know that slope of the velocity vector, if x’(t) is not 0, is given by y’(t)/x’(t) and this has to be equal to the slope f’ evaluated at x(t). Thus f’(x(t)) = y’(t)/x’(t) and y’(t) = f’(x(t))x’(t).

[D]

Exercises

1. Show directly that if y(t) = (x(t))², then y’(t) = 2x(t)x’(t), and in general if y(t) = x(t)^(p/q) for a rational number p/q, then y’(t) = (p/q)x(t)^(p/q-1)x’(t)

Differentiability2D 3D Parametric Equations Top of Page Contents

We now wish to give a geometric interpretation of the differentiability condition analogous to the one for continuity.

In the case of continuity, the challenge was to find δ sufficiently small that the graph of f over the interval of radius δ centered at x₀ would between the horizontal lines at height f(x₀) + ε and f(x₀) – ε. For differentiability, there is a stronger condition, namely that for sufficiently small δ,
|f(x) – f’(x₀)(x-x₀) – f(x₀)|/|x-x₀| < ε, i.e. –ε|x-x₀| < f(x) – f(x₀) - f’(x₀)(x-x₀) < ε|x-x₀|. This is equivalent to
f(x₀) + (f’(x₀) –ε)(x-x₀) < f(x) < f(x₀) + (f’(x₀) –ε)(x-x₀) and this is the condition that
the graph of f above the δ interval centered at x₀ should lie between the lines f(x₀) - (f’(x₀)+ε)(x-x₀) and f(x₀) + (f’(x) + ε)(x-x₀).

[D]

Exercises

Use the demonstrations for continuity and differentiability in one variable to show why differentiability at a point implies continuity at a point.